题目内容
(2012•丰台区一模)已知x2+3x-1=0,求代数式
•
-
的值.
| 1 |
| x-2 |
| x2-4x+4 |
| x+1 |
| x-1 |
| x+2 |
分析:先把分子和分母因式分解得到原式=
•
-
,然后约分后进行通分得到-
,再变形x2+3x-1=0得到x2+3x=1,最后整体代入计算即可.
| 1 |
| x-2 |
| (x-2)2 |
| x+1 |
| x-1 |
| x+2 |
| 3 |
| x2+3x+2 |
解答:解:原式=
•
-
=
-
=
=-
=-
,
∵x2+3x-1=0,
∴x2+3x=1,
∴原式=-
=-1.
| 1 |
| x-2 |
| (x-2)2 |
| x+1 |
| x-1 |
| x+2 |
=
| x-2 |
| x+1 |
| x-1 |
| x+2 |
=
| x2-4-x2+1 |
| (x+1)(x+2) |
=-
| 3 |
| (x+1)(x+2) |
=-
| 3 |
| x2+3x+2 |
∵x2+3x-1=0,
∴x2+3x=1,
∴原式=-
| 3 |
| 1+2 |
点评:本题考查了分式的化简求值:先进行分式的乘除运算(把分子或分母因式分解,约分),再进行分式的加减运算(即通分),然后把字母的值代入(或整体代入)进行计算.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
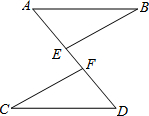 (2012•丰台区一模)已知:如图,AB∥CD,AB=CD,点E、F在线段AD上,且AF=DE.求证:BE=CF.
(2012•丰台区一模)已知:如图,AB∥CD,AB=CD,点E、F在线段AD上,且AF=DE.求证:BE=CF.