ƒøƒ⁄»›
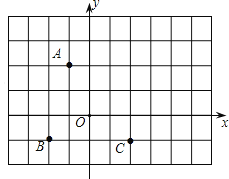
°æƒø°ø£®≤Ÿ◊˜∑¢œ÷£©»ÁÕº1£¨![]() Œ™µ»—¸÷±Ω«»˝Ω«–Œ£¨
Œ™µ»—¸÷±Ω«»˝Ω«–Œ£¨![]() £¨œ»Ω´»˝Ω«∞µƒ
£¨œ»Ω´»˝Ω«∞µƒ![]() Ω«”Î
Ω«”Î![]() ÷ÿ∫œ£¨‘ŸΩ´»˝Ω«∞»∆µ„
÷ÿ∫œ£¨‘ŸΩ´»˝Ω«∞»∆µ„![]() ∞¥À≥ ±’Î∑ΩœÚ–˝◊™£®–˝◊™Ω«¥Û”⁄
∞¥À≥ ±’Î∑ΩœÚ–˝◊™£®–˝◊™Ω«¥Û”⁄![]() «“–°”⁄
«“–°”⁄![]() £©£¨–˝◊™∫Û»˝Ω«∞µƒ“ª÷±Ω«±fl”Î
£©£¨–˝◊™∫Û»˝Ω«∞µƒ“ª÷±Ω«±fl”Î![]() Ωª”⁄µ„
Ωª”⁄µ„![]() £Æ‘⁄»˝Ω«∞¡̓ª÷±Ω«±fl…œ»°“ªµ„
£Æ‘⁄»˝Ω«∞¡̓ª÷±Ω«±fl…œ»°“ªµ„![]() £¨ π
£¨ π![]() £¨œfl∂Œ
£¨œfl∂Œ![]() …œ»°µ„
…œ»°µ„![]() £¨ π
£¨ π![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £¨
£¨![]() £Æ
£Æ

£®1£©«Î«Û≥ˆ![]() µƒ∂» ˝£ø
µƒ∂» ˝£ø
£®2£©![]() ”Î
”Î![]() œ‡µ»¬£ø«ÎÀµ√˜¿Ì”…£ª
œ‡µ»¬£ø«ÎÀµ√˜¿Ì”…£ª
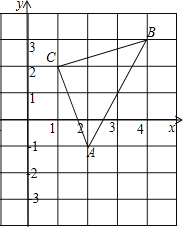
£®¿‡±»ÃΩæø£©»ÁÕº2£¨![]() Œ™µ»±fl»˝Ω«–Œ£¨œ»Ω´»˝Ω«∞Â÷–µƒ
Œ™µ»±fl»˝Ω«–Œ£¨œ»Ω´»˝Ω«∞Â÷–µƒ![]() Ω«”Î
Ω«”Î![]() ÷ÿ∫œ£¨‘ŸΩ´»˝Ω«∞»∆µ„
÷ÿ∫œ£¨‘ŸΩ´»˝Ω«∞»∆µ„![]() ∞¥À≥ ±’Î∑ΩœÚ–˝◊™£®–˝◊™Ω«¥Û”⁄
∞¥À≥ ±’Î∑ΩœÚ–˝◊™£®–˝◊™Ω«¥Û”⁄![]() «“–°”⁄
«“–°”⁄![]() £©.–˝◊™∫Û»˝Ω«∞µƒ“ª÷±Ω«±fl”Î
£©.–˝◊™∫Û»˝Ω«∞µƒ“ª÷±Ω«±fl”Î![]() Ωª”⁄µ„
Ωª”⁄µ„![]() .‘⁄»˝Ω«∞–±±fl…œ»°“ªµ„
.‘⁄»˝Ω«∞–±±fl…œ»°“ªµ„![]() £¨ π
£¨ π![]() £¨œfl∂Œ
£¨œfl∂Œ![]() …œ»°µ„
…œ»°µ„![]() £¨ π
£¨ π![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £¨
£¨![]() .
.
£®3£©÷±Ω”–¥≥ˆ![]() _________∂»£ª
_________∂»£ª
£®4£©»Ù![]() £¨
£¨![]() £¨«Ûœfl∂Œ
£¨«Ûœfl∂Œ![]() µƒ≥§∂».
µƒ≥§∂».
°æ¥∞∏°ø£®1£©![]() £ª£®2£©œ‡µ»£¨¿Ì”…œÍº˚Ω‚Œˆ£ª£®3£©
£ª£®2£©œ‡µ»£¨¿Ì”…œÍº˚Ω‚Œˆ£ª£®3£©![]() £ª£®4£©
£ª£®4£©![]()
°æΩ‚Œˆ°ø
£®1£©∏˘æ›»´µ»»˝Ω«–Œµƒ≈–∂®µ√≥ˆ![]() £¨‘Ÿ”…»´µ»»˝Ω«–Œµƒ–‘÷ µ√µΩ
£¨‘Ÿ”…»´µ»»˝Ω«–Œµƒ–‘÷ µ√µΩ![]() °¢
°¢![]() £¨»ª∫Û∏˘æ›µ»—¸»˝Ω«–Œµƒ≈–∂®∫Õ–‘÷ º¥ø…µ√Ω‚£ª
£¨»ª∫Û∏˘æ›µ»—¸»˝Ω«–Œµƒ≈–∂®∫Õ–‘÷ º¥ø…µ√Ω‚£ª
£®2£©∏˘æ›»´µ»»˝Ω«–Œµƒ≈–∂®µ√≥ˆ![]() £¨‘Ÿ”…»´µ»»˝Ω«–Œµƒ–‘÷ µ√÷§Ω·¬€£ª
£¨‘Ÿ”…»´µ»»˝Ω«–Œµƒ–‘÷ µ√÷§Ω·¬€£ª
£®3£©∏˘æ›»´µ»»˝Ω«–Œµƒ≈–∂®µ√≥ˆ![]() £¨‘Ÿ”…»´µ»»˝Ω«–Œµƒ–‘÷ µ√µΩ
£¨‘Ÿ”…»´µ»»˝Ω«–Œµƒ–‘÷ µ√µΩ![]() °¢
°¢![]() £¨»ª∫Û∏˘æ›µ»±fl»˝Ω«–Œµƒ≈–∂®∫Õ–‘÷ º¥ø…µ√Ω‚£ª
£¨»ª∫Û∏˘æ›µ»±fl»˝Ω«–Œµƒ≈–∂®∫Õ–‘÷ º¥ø…µ√Ω‚£ª
£®4£©π˝µ„![]() ◊˜
◊˜![]() ”⁄µ„
”⁄µ„![]() Ωª
Ωª![]() —”≥§œfl”⁄µ„
—”≥§œfl”⁄µ„![]() £¨ππ‘Ï≥ˆ
£¨ππ‘Ï≥ˆ![]() £¨¿˚”√∫¨
£¨¿˚”√∫¨![]() Ω«µƒ÷±Ω«»˝Ω«–Œµƒ–‘÷ «Ûµ√
Ω«µƒ÷±Ω«»˝Ω«–Œµƒ–‘÷ «Ûµ√![]() £¨‘Ÿ∏˘æ›π¥π…∂®¿Ì«Ûµ√
£¨‘Ÿ∏˘æ›π¥π…∂®¿Ì«Ûµ√![]() £¨◊Ó∫Û”…π¥π…∂®¿Ìº¥ø…«Ûµ√¥∞∏£Æ
£¨◊Ó∫Û”…π¥π…∂®¿Ìº¥ø…«Ûµ√¥∞∏£Æ
Ω‚£∫£®1£©°fl![]() Œ™µ»—¸÷±Ω«»˝Ω«–Œ£¨«“
Œ™µ»—¸÷±Ω«»˝Ω«–Œ£¨«“![]()
°‡![]() £¨
£¨![]()
°fl![]()
°‡![]()
°‡![]()
‘⁄![]() ∫Õ
∫Õ![]() ÷–£¨
÷–£¨
°‡![]()
°‡![]() £¨
£¨![]()
°‡![]() £ª
£ª
£®2£©œ‡µ»£¨¿Ì”…»Áœ¬£∫
°fl![]() £¨
£¨![]()
°‡![]()
°‡![]()
‘⁄![]() ∫Õ
∫Õ![]() ÷–£¨
÷–£¨
°‡![]()
°‡ ![]() £Æ
£Æ
£®3£©°fl![]() Œ™µ»±fl»˝Ω«–Œ
Œ™µ»±fl»˝Ω«–Œ
°‡![]() £¨
£¨![]()
°fl![]()
°‡![]()
°‡![]()
‘⁄![]() ∫Õ
∫Õ![]() ÷–£¨
÷–£¨
°‡![]()
°‡![]()
°‡![]() £ª
£ª
£®4£©π˝µ„![]() ◊˜
◊˜![]() ”⁄µ„
”⁄µ„![]() Ωª
Ωª![]() —”≥§œfl”⁄µ„
—”≥§œfl”⁄µ„![]() £¨»ÁÕº£∫
£¨»ÁÕº£∫

°fl”…£®3£©ø…÷™£¨![]() £¨
£¨![]()
°‡![]() £¨
£¨![]()
°‡![]()
°‡![]()
°‡![]() £¨
£¨![]()
°‡![]() £Æ
£Æ

°æƒø°øŒ™¡ÀΩ‚ƒ≥–£—ß…˙∂‘°∂◊Ó«ø¥Ûƒ‘°∑°¢°∂¿ ∂¡’fl°∑°¢°∂÷–π˙ ´¥ ¥Ûª·°∑°¢°∂≥ˆ≤ ÷–π˙»À°∑Àƒ∏ˆµÁ ”Ω⁄ƒøµƒœ≤∞Æ«Èøˆ£¨Àʪ˙≥È»°¡À![]() √˚—ß…˙Ω¯––µ˜≤ÈÕ≥º∆£®“™«Û√ø√˚—ß…˙—°≥ˆ≤¢«“÷ªƒ‹—°≥ˆ“ª∏ˆ◊‘º∫◊Óœ≤∞ƵƒΩ⁄ƒø£©£¨≤¢Ω´µ˜≤ÈΩ·π˚ªÊ÷∆≥…»Áœ¬Õ≥º∆Õº±Ì:
√˚—ß…˙Ω¯––µ˜≤ÈÕ≥º∆£®“™«Û√ø√˚—ß…˙—°≥ˆ≤¢«“÷ªƒ‹—°≥ˆ“ª∏ˆ◊‘º∫◊Óœ≤∞ƵƒΩ⁄ƒø£©£¨≤¢Ω´µ˜≤ÈΩ·π˚ªÊ÷∆≥…»Áœ¬Õ≥º∆Õº±Ì:

—ß…˙◊Óœ≤ª∂µƒΩ⁄ƒø»À ˝Ãı–ŒÕ≥º∆Õº
Ω⁄ƒø | »À ˝( √˚ ) | ∞Ÿ∑÷±» |
◊Ó«ø¥Ûƒ‘ | 5 | 10% |
¿ ∂¡’fl | 15 |
|
÷–π˙ ´¥ ¥Ûª· |
| 40% |
≥ˆ≤ ÷–π˙»À | 10 | 20% |
—ß…˙◊Óœ≤∞ƵƒΩ⁄ƒø»À ˝Õ≥º∆±Ì
∏˘æ›“‘…œÃ·π©µƒ–≈œ¢£¨Ω‚¥œ¬¡–Œ Â:
£®1£©![]() =
= ![]() =
= ![]() = £ª
= £ª
£®2£©≤π»´Ãı–ŒÕ≥º∆Õº£ª
£®3£©»Ù∏√–£π≤”–—ß…˙1200√˚£¨∏˘æ›≥È—˘µ˜≤ÈΩ·π˚£¨π¿º∆∏√–£◊Óœ≤∞Æ°∂÷–π˙ ´¥ ¥Ûª·°∑Ω⁄ƒøµƒ—ß…˙”–∂‡…Ÿ√˚£ø