题目内容
在△ABC中，点D，E分别在AB，AC上，且CD与BE相交于点F，已知△BDF的面积为10，△BCF的面积为20，△CEF的面积为16，则四边形区域ADFE的面积等于
- A.22
- B.24
- C.36
- D.44
D
分析：可设S△ADF=m，根据题中条件可得出三角形的面积与边长之间的关系，进而用m表示出△AEF，求出m的值，进而可得四边形的面积．
解答：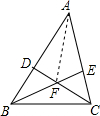
解：如图，连AF，设S△ADF=m，
∵S△BDF：S△BCF=10：20=1：2=DF：CF，
则有2m=S△AEF+S△EFC，
S△AEF=2m-16，
而S△BFC：S△EFC=20：16=5：4=BF：EF，
又∵S△ABF：S△AEF=BF：EF=5：4，
而S△ABF=m+S△BDF=m+10，
∴S△ABF：S△AEF=BF：EF=5：4=（m+10）：（2m-16），
解得m=20．
S△AEF=2×20-16=24，
SADEF=S△AEF+S△ADF=24+20=44．
故选D．
点评：本题主要考查了三角形的面积计算问题，能够利用三角形的性质进行一些简单的计算．
分析：可设S△ADF=m，根据题中条件可得出三角形的面积与边长之间的关系，进而用m表示出△AEF，求出m的值，进而可得四边形的面积．
解答：
解：如图，连AF，设S△ADF=m，∵S△BDF：S△BCF=10：20=1：2=DF：CF，
则有2m=S△AEF+S△EFC，
S△AEF=2m-16，
而S△BFC：S△EFC=20：16=5：4=BF：EF，
又∵S△ABF：S△AEF=BF：EF=5：4，
而S△ABF=m+S△BDF=m+10，
∴S△ABF：S△AEF=BF：EF=5：4=（m+10）：（2m-16），
解得m=20．
S△AEF=2×20-16=24，
SADEF=S△AEF+S△ADF=24+20=44．
故选D．
点评：本题主要考查了三角形的面积计算问题，能够利用三角形的性质进行一些简单的计算．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
∠ACB的外角平分线于点F．
如图，在△ABC中，点D，E分别在边AB，AC上，给出5个论断：①CD⊥AB；②BE⊥AC；③AE=CE；④∠ABE=30°；⑤CD=BE．
（2013•上海）如图，已知在△ABC中，点D、E、F分别是边AB、AC、BC上的点，DE∥BC，EF∥AB，且AD：DB=3：5，那么CF：CB等于（ ）