题目内容
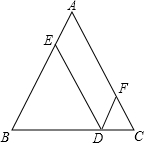 如图,在△ABC,AB=AC=a,点D是BC边上一点DE∥AC,DF∥AB,则四边形AEDF的周长为________.
如图,在△ABC,AB=AC=a,点D是BC边上一点DE∥AC,DF∥AB,则四边形AEDF的周长为________.
2a
分析:由DE平行于AC,DF平行于AB,利用两组对边平行的四边形是平行四边形,得到AEDF为平行四边形,根据平行四边形的对边相等可得出AE=FD,AF=ED,由AB与FD平行,利用两直线平行同位角相等得到一对角相等,再由AB=AC,利用等边对等角得到一对角相等,等量代换可得出∠FDC=∠FCD,利用等角对等边得到FD=FC,由平行四边形的周长等于四条边相加,等量代换得到2(AE+AF),再将AE换为FC,由AF+FC=AC,可表示出平行四边形的周长.
解答:∵DE∥AC,DF∥AB,
∴四边形AEDF为平行四边形,∠B=∠FDC,
∴AE=FD,AF=ED,
∵AB=AC=a,
∴∠B=∠C,
∴∠FDC=∠FCD,
∴FD=FC,
∴AE=FC,
∴平行四边形AEDF的周长为AE+ED+DF+AF=2(AE+AF)=2(AF+FC)=2AC=2a.
故答案为:2a.
点评:此题考查了等腰三角形的判定与性质,平行四边形的判定与性质,以及平行线的性质,利用了转化及等量代换的数学思想,熟练掌握判定与性质是解本题的关键.
分析:由DE平行于AC,DF平行于AB,利用两组对边平行的四边形是平行四边形,得到AEDF为平行四边形,根据平行四边形的对边相等可得出AE=FD,AF=ED,由AB与FD平行,利用两直线平行同位角相等得到一对角相等,再由AB=AC,利用等边对等角得到一对角相等,等量代换可得出∠FDC=∠FCD,利用等角对等边得到FD=FC,由平行四边形的周长等于四条边相加,等量代换得到2(AE+AF),再将AE换为FC,由AF+FC=AC,可表示出平行四边形的周长.
解答:∵DE∥AC,DF∥AB,
∴四边形AEDF为平行四边形,∠B=∠FDC,
∴AE=FD,AF=ED,
∵AB=AC=a,
∴∠B=∠C,
∴∠FDC=∠FCD,
∴FD=FC,
∴AE=FC,
∴平行四边形AEDF的周长为AE+ED+DF+AF=2(AE+AF)=2(AF+FC)=2AC=2a.
故答案为:2a.
点评:此题考查了等腰三角形的判定与性质,平行四边形的判定与性质,以及平行线的性质,利用了转化及等量代换的数学思想,熟练掌握判定与性质是解本题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 的顶点D放在AB边上,E、F分别在AC、BC上,当点D在AB边上移动时,DE始终与AB垂直.
的顶点D放在AB边上,E、F分别在AC、BC上,当点D在AB边上移动时,DE始终与AB垂直.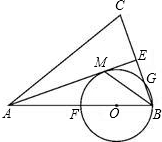 F,FB恰为⊙O的直径.
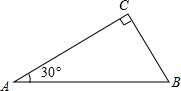
F,FB恰为⊙O的直径. 7、如图,在△ABC中,D是BC上的一点,∠C=62°,∠CAD=32°,则∠ADB=
7、如图,在△ABC中,D是BC上的一点,∠C=62°,∠CAD=32°,则∠ADB=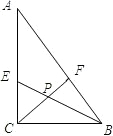 如图,在△ABC中,∠ACB=90°,BE平分∠ABC,CF平分∠ACB,CF,BE交于点P,AC=4cm,BC=3cm,AB=5cm,则△CPB的面积为
如图,在△ABC中,∠ACB=90°,BE平分∠ABC,CF平分∠ACB,CF,BE交于点P,AC=4cm,BC=3cm,AB=5cm,则△CPB的面积为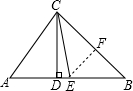 如图,在△ABC中,CD是高,CE为∠ACB的平分线.若AC=15,BC=20,CD=12,EF∥AC,则∠CEF的大小为
如图,在△ABC中,CD是高,CE为∠ACB的平分线.若AC=15,BC=20,CD=12,EF∥AC,则∠CEF的大小为