题目内容
【题目】如图甲,在平面直角坐标系中,直线分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() 、
、![]() ,⊙
,⊙![]() 的半径为
的半径为![]() 个单位长度,点
个单位长度,点![]() 为直线
为直线![]() 上的动点,过点
上的动点,过点![]() 作⊙
作⊙![]() 的切线
的切线![]() 、
、![]() ,切点分别为
,切点分别为![]() 、
、![]() ,且
,且![]() .
.
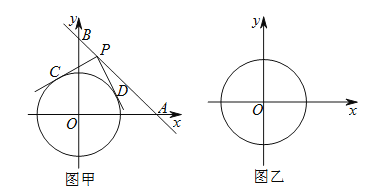
(1)判断四边形![]() 的形状并说明理由.
的形状并说明理由.
(2)求点![]() 的坐标.
的坐标.
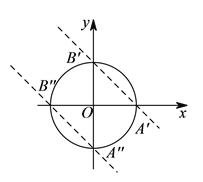
(3)若直线![]() 沿
沿![]() 轴向左平移得到一条新的直线
轴向左平移得到一条新的直线![]() ,此直线将⊙
,此直线将⊙![]() 的圆周分得两段弧长之比为
的圆周分得两段弧长之比为![]() ,请直接写出
,请直接写出![]() 的值.
的值.
(4)若将⊙![]() 沿
沿![]() 轴向右平移(圆心
轴向右平移(圆心![]() 始终保持在
始终保持在![]() 轴上),试写出当⊙
轴上),试写出当⊙![]() 与直线
与直线![]() 有交点时圆心
有交点时圆心![]() 的横坐标
的横坐标![]() 的取值范围.(直接写出答案)
的取值范围.(直接写出答案)
【答案】(1)OCPD是正方形;(2)(2,4)或(4,2);(3)±![]() ;(4)
;(4)![]() .
.
【解析】试题分析: (1)四边形OCPD是正方形.如图,连接OC、OD.根据切线的性质和已知条件得知四边形OCPD的三个内角是90°,则该四边形是矩形.又由OC=OD,所以四边形OCPD是正方形;(2)连接OP,由![]() 为正方形,可得
为正方形,可得![]() ,设
,设![]() ,由
,由![]() 和勾股定理可得
和勾股定理可得![]() ,解得:
,解得:![]() 或
或![]() .所以
.所以![]() 点坐标为
点坐标为![]() 或
或![]() ;(3)已知平移后的新直线
;(3)已知平移后的新直线![]() 交圆于
交圆于![]() ,分得的两段弧长之比为
,分得的两段弧长之比为![]() ,可知分得的劣弧是圆周的
,可知分得的劣弧是圆周的![]() ,因直线
,因直线![]() 与
与![]() 轴夹角为
轴夹角为![]() ,
,![]() ,可得
,可得![]() ,所以当
,所以当![]() 为
为![]() 圆周时,直线与坐标轴的交点恰好是⊙
圆周时,直线与坐标轴的交点恰好是⊙![]() 与坐标轴的交点,
与坐标轴的交点,
即可得当![]() 平移到
平移到![]() 位置时,
位置时,![]() ;当
;当![]() 平移到
平移到![]() 位置时,
位置时,![]() ,所以
,所以
![]() 的值为
的值为![]() 或
或![]() ;(4)如图,⊙
;(4)如图,⊙![]() 沿
沿![]() 轴向右平移过程中分别在⊙
轴向右平移过程中分别在⊙![]() 处,⊙
处,⊙![]() 处与直线
处与直线![]() 相切,则圆在
相切,则圆在![]() 落在
落在![]() ,
,![]() 之间均满足题意,由此即可求得圆心
之间均满足题意,由此即可求得圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
试题解析:
(![]() )四边形
)四边形![]() 为正方形.
为正方形.
理由如下:连接![]() 、
、![]() ,易知
,易知![]() ,
,![]() ,
,
又![]() ,
,
∴四边形![]() 为矩形,
为矩形,
又![]() ,
,
∴四边形![]() 为正方形.
为正方形.

(![]() )连接
)连接![]() ,
,
∵![]() 为正方形,
为正方形,
∴![]() ,
,
∵![]() 在直线
在直线![]() 上,
上,
设![]() ,
,
由![]() 得:
得:
![]() ,
,
解得:![]() 或
或![]() .
.
∴![]() 点坐标为
点坐标为![]() 或
或![]() .
.
(![]() )平移后的新直线
)平移后的新直线![]() 交圆于
交圆于![]() ,分得的两段弧长之比为
,分得的两段弧长之比为![]() ,
,
∴分得的劣弧是圆周的![]() ,
,
∵直线![]() 与
与![]() 轴夹角为
轴夹角为![]() ,
,![]() ,
,
∴![]() ,
,
当![]() 为
为![]() 圆周时,直线与坐标轴的交点恰好是⊙
圆周时,直线与坐标轴的交点恰好是⊙![]() 与坐标轴的交点,
与坐标轴的交点,
当![]() 平移到
平移到![]() 位置时,
位置时,![]() ;
;
当![]() 平移到
平移到![]() 位置时,
位置时,![]() ,
,
∴![]() 的值为
的值为![]() 或
或![]() .
.
(![]() )如图,⊙
)如图,⊙![]() 沿
沿![]() 轴向右平移过程中分别在⊙
轴向右平移过程中分别在⊙![]() 处,⊙
处,⊙![]() 处与直线
处与直线![]() 相切,
相切,
则圆在![]() 落在
落在![]() ,
,![]() 之间均满足题意,
之间均满足题意,
在⊙![]() 处相切时,
处相切时,![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,![]() .
.
∴![]() ,同理,在⊙
,同理,在⊙![]() 处相切时,
处相切时,![]() ,
,
∴![]() ,
,
∴当⊙![]() 与直线
与直线![]() 有交点时,圆心
有交点时,圆心![]() 的横坐标
的横坐标![]() 的取值范围为
的取值范围为![]() .
.
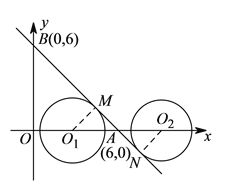

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案