题目内容
如图,P为正方形ABCD边BC上任一点,BG⊥AP于点G,在AP的延长线上取点E,使AG=GE,连接BE,CE.(1)求证:BE=BC;
(2)∠CBE的平分线交AE于N点,连接DN,求证:BN+DN=
| 2 |
(3)若正方形的边长为2,当P点为BC的中点时,请直接写出CE的长为

分析:(1)BG垂直平分线段AE,根据线段垂直平分线上的点到两端点的距离相等,AB=BE,又AB=BC,所以BE=BC;
(2)标准答案上仅用等腰三角形和直角三角形通过∠GBP+∠PBN=∠GBN=∠PNB=∠NBE+∠NEB,得出Rt△BPG是等腰直角三角形,进而得到,AM=GN;
(3)先求出BG的长度,根据P为BC的中点,CN=BG,再根据△CNE为等腰直角三角形即可求出CE的长度.
(2)标准答案上仅用等腰三角形和直角三角形通过∠GBP+∠PBN=∠GBN=∠PNB=∠NBE+∠NEB,得出Rt△BPG是等腰直角三角形,进而得到,AM=GN;
(3)先求出BG的长度,根据P为BC的中点,CN=BG,再根据△CNE为等腰直角三角形即可求出CE的长度.
解答:(1)证明:∵BG⊥AP,AG=GE,
∴BG垂直平分线段AE,
∴AB=BE,
在正方形ABCD中,AB=BC,
∴BE=BC;
(2)证明:连接CN,延长BN交CE于H.
自点D作DM⊥AN于M,
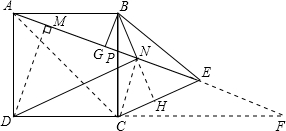
显然Rt△ADM≌Rt△ABG,DM=AG,
∵BN平分∠CBE,∴CH=HE,
∵∠CBN=∠EBN,BE=BC,BN=BN,
∴△BCN≌△BEN,
∴CN=NE,△CEN是等腰三角形,
延长AE交DC延长线于F,则有:∠BAG=∠BEG=∠CFE=∠BCN,
A,B,C,D,N五点共圆,∠AND=∠BNG=45°[AB弦所对圆周角=45°]
Rt△DMN,Rt△BGN都是等腰直角三角形,
DM=
AG=DN,
GN=BN,
AG+
GN=
AN=BN+DN;
(3)根据勾股定理,AP=
=
=
,
∴BG=
=
,
∵BP=PC,∠BGP=∠CNP=90°,
∴△BPG≌△CNP(AAS),
∴CN=BG,
∴CE=
CN=
×
=
.
∴BG垂直平分线段AE,
∴AB=BE,
在正方形ABCD中,AB=BC,
∴BE=BC;
(2)证明:连接CN,延长BN交CE于H.
自点D作DM⊥AN于M,

显然Rt△ADM≌Rt△ABG,DM=AG,
∵BN平分∠CBE,∴CH=HE,
∵∠CBN=∠EBN,BE=BC,BN=BN,
∴△BCN≌△BEN,
∴CN=NE,△CEN是等腰三角形,
延长AE交DC延长线于F,则有:∠BAG=∠BEG=∠CFE=∠BCN,
A,B,C,D,N五点共圆,∠AND=∠BNG=45°[AB弦所对圆周角=45°]
Rt△DMN,Rt△BGN都是等腰直角三角形,
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
(3)根据勾股定理,AP=
| AB2+BP2 |
| 22+12 |
| 5 |
∴BG=
| 2×1 | ||
|
2
| ||
| 5 |
∵BP=PC,∠BGP=∠CNP=90°,
∴△BPG≌△CNP(AAS),
∴CN=BG,
∴CE=
| 2 |
| 2 |
2
| ||
| 5 |
2
| ||
| 5 |
点评:本题综合性较强,主要利用线段垂直平分线段判定和性质,等腰直角三角形的性质,全等三角形的判定和性质,勾股定理,综合运用各定理和性质,并分析题目用已知条件和所要证明的结论之间的关系是解本题的关键,准确作出辅助线对解决本题非常重要,需要同学们在平时的学习中不断提高自我并完善各知识点之间的联系,本题难度较大.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 17、如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合.
17、如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合. OM方向以
OM方向以 向以
向以
 (2009•梅州一模)如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙0与BC相切于点M,与AB、AD分别相交于点E、F.
(2009•梅州一模)如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙0与BC相切于点M,与AB、AD分别相交于点E、F.