ЬтФПФкШн
ЁОЬтФПЁПдФЖСгыгІгУЃКЭЌбЇУЧЃЌФуУЧвбОжЊЕР![]() ЃЌМД
ЃЌМД![]() ЃЎЫљвд
ЃЎЫљвд![]() ЃЈЕБЧвНіЕБ
ЃЈЕБЧвНіЕБ![]() ЪБШЁЕШКХЃЉЃЎ
ЪБШЁЕШКХЃЉЃЎ
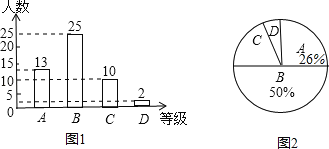
дФЖС1ЃКШє![]() ЮЊЪЕЪ§ЃЌЧв
ЮЊЪЕЪ§ЃЌЧв![]() ЃЈЕБЧвНіЕБ
ЃЈЕБЧвНіЕБ![]() ЪБШЁЕШКХЃЉЃЎ
ЪБШЁЕШКХЃЉЃЎ
дФЖС2ЃКШєКЏЪ§![]() ЃЈ
ЃЈ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊГЃЪ§ЃЉЃЎгЩдФЖС1НсТлПЩжЊЃК
ЮЊГЃЪ§ЃЉЃЎгЩдФЖС1НсТлПЩжЊЃК![]() МД
МД![]() ЃЌЁрЕБ
ЃЌЁрЕБ![]() МД
МД![]() ЪБЃЌКЏЪ§
ЪБЃЌКЏЪ§![]() ЕФзюаЁжЕЮЊ
ЕФзюаЁжЕЮЊ![]() ЃЎ
ЃЎ
дФЖСРэНтЩЯЪіФкШнЃЌНтД№ЯТСаЮЪЬтЃК
ЮЪЬт1ЃКШєКЏЪ§![]() ЃЌдђ
ЃЌдђ![]() = ЪБЃЌКЏЪ§
= ЪБЃЌКЏЪ§![]() ЕФзюаЁжЕЮЊ ЃЎ
ЕФзюаЁжЕЮЊ ЃЎ
ЮЪЬт2ЃКвбжЊвЛИіОиаЮЕФУцЛ§ЮЊ4ЃЌЦфжавЛБпГЄЮЊ![]() ЃЌдђСэвЛБпГЄЮЊ
ЃЌдђСэвЛБпГЄЮЊ![]() ЃЌжмГЄЮЊ
ЃЌжмГЄЮЊ![]() ЃЌЧѓЕБ
ЃЌЧѓЕБ![]() ЪБЃЌОиаЮжмГЄЕФзюаЁжЕЮЊ ЃЎ
ЪБЃЌОиаЮжмГЄЕФзюаЁжЕЮЊ ЃЎ
ЮЪЬт3ЃКЧѓДњЪ§ЪН![]() ЕФзюаЁжЕЃЎ
ЕФзюаЁжЕЃЎ
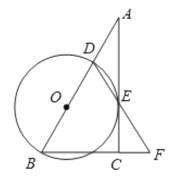
ЮЪЬт4ЃКНЈдьвЛИіШнЛ§ЮЊ8СЂЗНУзЃЌЩю2УзЕФГЄЗНЬхЮоИЧЫЎГиЃЌГиЕзКЭГиБкЕФдьМлЗжБ№ЮЊУПЦНЗНУз![]() УзЃЌЫЎГизмдьМлЮЊ
УзЃЌЫЎГизмдьМлЮЊ![]() ЃЈдЊЃЉЃЌЧѓЕБ
ЃЈдЊЃЉЃЌЧѓЕБ![]() ЮЊЖрЩйЪБЃЌЫЎГизмдьМл
ЮЊЖрЩйЪБЃЌЫЎГизмдьМл![]() зюЕЭЃПзюЕЭЪЧЖрЩйЃП
зюЕЭЃПзюЕЭЪЧЖрЩйЃП
ЁОД№АИЁПЮЪЬт1ЃК![]() ЃЛ
ЃЛ![]() ЮЪЬт2ЃК
ЮЪЬт2ЃК![]() ЃЛ
ЃЛ![]() ЮЪЬт3ЃК
ЮЪЬт3ЃК![]() ЮЪЬт4ЃКЕБ
ЮЪЬт4ЃКЕБ![]() ЪБЃЌЫЎГизмдьМл
ЪБЃЌЫЎГизмдьМл![]() зюЕЭЃЌзюЕЭЮЊ
зюЕЭЃЌзюЕЭЮЊ![]() дЊ
дЊ
ЁОНтЮіЁП
ЮЪЬт1ЃКИљОндФЖСВФСЯНтОіЮЪЬтМДПЩЃЛ
ЮЪЬт2ЃКИљОнОиаЮЕФаджЪКЭдФЖСВФСЯФкШнНјааМЦЫуМДПЩЧѓНтЃЛ
ЮЪЬт3ЃКЯШНЋДњЪ§ЪНБфаЮЃЌдйИљОндФЖСФкШнМДПЩЧѓНтЃЛ
ЮЪЬт4ЃКИљОнСЂЗНЬхЕФЬхЛ§ЙЋЪНКЭвбжЊЬѕМўБэЪОГіГЄЗНЬхЕФПэЃЌдЫгУдФЖСФкШнМДПЩЧѓНтЃЎ
НтЃКЮЪЬт1ЃКЁп![]()
Ёр![]()
ЁргЩдФЖС2НсТлПЩжЊЃЌ![]() МД
МД![]()
ЁрЕБ![]() МД
МД![]()
Ёр![]() ЃЌ
ЃЌ![]() ЃЈВЛКЯЬтвтЩсШЅЃЉ
ЃЈВЛКЯЬтвтЩсШЅЃЉ
ЁрЕБ![]() ЪБЃЌКЏЪ§
ЪБЃЌКЏЪ§![]() ЕФзюаЁжЕЮЊ
ЕФзюаЁжЕЮЊ![]() ЃЛ
ЃЛ
ЮЪЬт2ЃКЩшОиаЮжмГЄЮЊ![]() ЃЌИљОнЬтвтЕУ
ЃЌИљОнЬтвтЕУ![]()
Ёп![]()
Ёр![]()
ЁрЕБ![]() МД
МД![]() ЃЈВЛКЯЬтвтЩсШЅЃЉЃЌ
ЃЈВЛКЯЬтвтЩсШЅЃЉЃЌ![]() ЪБЃЌКЏЪ§
ЪБЃЌКЏЪ§![]() газюаЁжЕ
газюаЁжЕ![]() ЃЛ
ЃЛ
ЮЪЬт3ЃКЁпЩш![]()
Ёр![]()
Ёп![]()
ЁрЕБ![]() МД
МД![]() ЃЈВЛКЯЬтвтЩсШЅЃЉЃЌ
ЃЈВЛКЯЬтвтЩсШЅЃЉЃЌ![]() ЪБЃЌКЏЪ§
ЪБЃЌКЏЪ§![]() газюаЁжЕ
газюаЁжЕ![]()
ЁрДњЪ§ЪН![]() ЕФзюаЁжЕЮЊ
ЕФзюаЁжЕЮЊ![]() ЃЛ
ЃЛ
ЮЪЬт4ЃКЁпИљОнЬтвтЕУГЄЗНЬхЕФПэЮЊ![]() Уз
Уз
Ёр![]()
Ёп![]()
ЁрЕБ![]() МД
МД![]() ЃЈВЛКЯЬтвтЩсШЅЃЉЃЌ
ЃЈВЛКЯЬтвтЩсШЅЃЉЃЌ![]() ЪБЃЌКЏЪ§
ЪБЃЌКЏЪ§![]() ЕФзюаЁжЕЮЊ
ЕФзюаЁжЕЮЊ![]()
ЁрЕБ![]() ЪБЃЌЫЎГизмдьМл
ЪБЃЌЫЎГизмдьМл![]() зюЕЭЃЌзюЕЭЮЊ
зюЕЭЃЌзюЕЭЮЊ![]() дЊЃЎ
дЊЃЎ
ЙЪД№АИЪЧЃКЮЪЬт1ЃК![]() ЃЛ
ЃЛ![]() ЮЪЬт2ЃК
ЮЪЬт2ЃК![]() ЃЛ
ЃЛ![]() ЮЪЬт3ЃК
ЮЪЬт3ЃК![]() ЮЪЬт4ЃКЕБ
ЮЪЬт4ЃКЕБ![]() ЪБЃЌЫЎГизмдьМл
ЪБЃЌЫЎГизмдьМл![]() зюЕЭЃЌзюЕЭЮЊ
зюЕЭЃЌзюЕЭЮЊ![]() дЊ
дЊ