Question

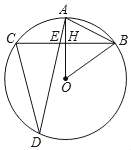
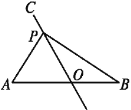
【题目】如图，某同学在一张硬纸板的中间画了一条4cm长的线段AB，过AB的中点O画直线CO，使∠AOC=60°，在直线CO上取一点P，作△PAB并剪下(纸板足够大)，当剪下的△PAB为直角三角形时，AP的长为_____.

Answer 1

【答案】2或2或2

【解析】

利用分类讨论，当∠ABP=90°时，如图2，由对顶角的性质可得∠AOC=∠BOP=60°，利用锐角三角函数可得BP的长，利用勾股定理可得AP的长；当∠APB=90°时，分两种情况讨论，情况一：如图1，利用直角三角形斜边的中线等于斜边的一半得出PO=BO，易得△BOP为等边三角形，利用锐角三角函数可得AP的长；情况二：如图3，利用直角三角形斜边的中线等于斜边的一半可得结论；当∠PAB=90°时，如图4，利用锐角三角函数即可得AP的长.

当∠APB=90°时，情况一（如图1）：

∵AO=BO，

∴PO=BO，

∵∠AOC=60°，

∴∠BOP=60°，

∴△BOP为等边三角形，

∴AP=ABsin60°=4×=2；

情况二：如图3，∵AO=BO，∠APB=90°，

∴PO=AO，

∵∠AOC=60°，

∴△AOP为等边三角形，

∴AP=AO=2，

当∠ABP=90°时（如图2），

∵∠AOC=∠BOP=60°，

∴BP=OBtan60°=2，

在直角三角形ABP中，

AP==2，

当∠PAB=90°时，如图4

∵∠AOC=60°，

∴AP=OAtan60°=2

故答案为：2或2或2．