题目内容
【题目】如图,在矩形ABCD中,AB=2,AD=3,点E是BC边上靠近点B的三等分点,动点P从点A出发,沿路径A→D→C→E运动,则△APE的面积y与点P经过的路径长x之间的函数关系用图象表示大致是( )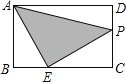
A.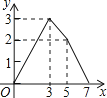
B.
C.
D.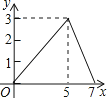
【答案】A
【解析】解:∵在矩形ABCD中,AB=2,AD=3,
∴CD=AB=2,BC=AD=3,
∵点E是BC边上靠近点B的三等分点,
∴CE=![]() ×3=2,
×3=2,
①点P在AD上时,△APE的面积y=![]() x2=x(0≤x≤3),
x2=x(0≤x≤3),
②点P在CD上时,S△APE=S梯形AECD﹣S△ADP﹣S△CEP ,
=![]() (2+3)×2﹣
(2+3)×2﹣![]() ×3×(x﹣3)﹣
×3×(x﹣3)﹣![]() ×2×(3+2﹣x),
×2×(3+2﹣x),
=5﹣![]() x+
x+![]() ﹣5+x,
﹣5+x,
=﹣![]() x+
x+![]() ,
,
∴y=﹣![]() x+
x+![]() (3<x≤5),
(3<x≤5),
③点P在CE上时,S△APE=![]() ×(3+2+2﹣x)×2=﹣x+7,
×(3+2+2﹣x)×2=﹣x+7,
∴y=﹣x+7(5<x≤7),
故选:A.
求出CE的长,然后分①点P在AD上时,利用三角形的面积公式列式得到y与x的函数关系;②点P在CD上时,根据S△APE=S梯形AECD﹣S△ADP﹣S△CEP列式整理得到y与x的关系式;③点P在CE上时,利用三角形的面积公式列式得到y与x的关系式,然后选择答案即可.

练习册系列答案
相关题目