题目内容
10、对于一个自然数n，如果能找到自然数a和b，使n=a+b+ab，则称n为一个“好”数，例如3=1+1+1×1，则3是一个“好”数，在1～～20这20个自然数中，“好”数有
12
个．分析：先根据合数的定义得出所求数均为合数少1的数，再找出1～～20这20个自然数中所有符合条件的合数求出比合数少1的数即可．
解答：解：n+1=a+b+ab+1=（a+1）（b+1）为合数，所求的n即为2～～～21之间的合数少1的数．
2～～21之间的合数有：4、6、8、9、10、12、14、15、16、18、1、20、21共12个，
故所求的n有12个．为3、5、7、8、9、10、11、13、14、15、17、19、20．
故答案为：12．
2～～21之间的合数有：4、6、8、9、10、12、14、15、16、18、1、20、21共12个，
故所求的n有12个．为3、5、7、8、9、10、11、13、14、15、17、19、20．
故答案为：12．
点评：本题考查的是质数与合数，解答此题的关键是把找出所求数与合数之间的关系，再根据合数的定义解答．
练习册系列答案
相关题目
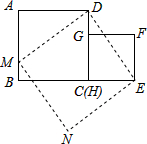【问题提出】如何把n个正方形拼接成一个大正方形？
；已知对于任意的实数x，记号[x]表示不超过x的最大整数；将英文字母转化成密码，如
，即h变成q，再如
，即k变成f．他们给出下列一组密码：etwcvcjwejncjwwcabqcv，把它翻译出来就是一句很好的临别赠言．现在就请你把它翻译出来，并简单地写出翻译过程．
；已知对于任意的实数x，记号[x]表示不超过x的最大整数；将英文字母转化成密码，如
，即h变成q，再如
，即k变成f．他们给出下列一组密码：etwcvcjwejncjwwcabqcv，把它翻译出来就是一句很好的临别赠言．现在就请你把它翻译出来，并简单地写出翻译过程．
；已知对于任意的实数x，记号[x]表示不超过x的最大整数；将英文字母转化成密码，如
，即h变成q，再如
，即k变成f．他们给出下列一组密码：etwcvcjwejncjwwcabqcv，把它翻译出来就是一句很好的临别赠言．现在就请你把它翻译出来，并简单地写出翻译过程．