Question

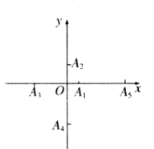
【题目】如图，在直角坐标系的坐标轴上按如下规律取点：在轴正半轴上，在轴正半轴上，在轴负半轴上，在轴负半轴上，在轴正半轴上，......，且......，设......,有坐标分别为，......，．

（1）当时，求的值；

（2）若，求的值；

（3）当时，直接写出用含为正整数)的式子表示轴负半轴上所取点．

Answer 1

【答案】（1），（2）；（3）

【解析】

（1）根据题意，分别的坐标依次写出，便能知道的值；

（2）由（1）中的规律能够得到与的关系，进而可表示出，再利用求得的值；

（3）先依次探究轴负半轴上所取点的坐标规律，进而得到答案．

解：∵，

∴，

∴，

（2）由（1）可知，，

∴

，

当时，，

∴；

（3）由题意可知，

当时，x轴负半轴上的点的坐标依次是，……

也就是说x轴负半轴上的点的纵坐标为0，横坐标依次减小4，

∴x轴负半轴上的点的坐标可以表示为