Question

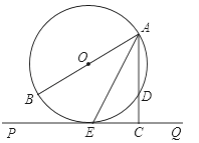
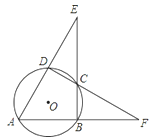
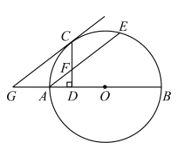
【题目】如图，AB是⊙O的直径，AE是弦，C是弧AE的中点，过点C作GC∥AE交BA的延长线于点G，过点C作CD⊥AB于点D，交AE于点F．

（1）判断GC与⊙O的位置关系，并证明.

（2）若sin∠EAB =，OD=，求AE的长．

Answer 1

【答案】（1）相切.证明见解析；（2）

【解析】

（1）连接OC，根据垂径定理得到OC⊥AE，又GC∥AE得到OC⊥GC，即可判定；

（2）根据OC⊥AE,CD⊥AB得到∠OCD=∠EAB，利用求得

，故，连接BE，根据直径的性质得到∠AEB=90°，利用在Rt△AEB中，，求出，即可求出.

（1）相切.

证明：连接OC，交AE于H.

∵C是弧AE的中点，

∴OC⊥AE.

∵GC∥AE.

∴OC⊥GC.

∴GC是⊙O的切线.

（2）解： ∵OC⊥AE ,CD⊥AB,

∴∠OCD=∠EAB.

∴.

在Rt△CDO中，OD=，

∴.

∴.

连接BE.

∵AB是⊙O的直径，

∴∠AEB=90°.在Rt△AEB中，

∵,

∴.

∴.