题目内容
如图,在等腰△ABC中,AB=BC,∠A=30°将△ABC绕点B顺时针旋转30°,得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点.
(1)证明:△ABE≌△C1BF;
(2)证明:EA1=FC;
(3)试判断四边形ABC1D的形状,并说明理由.

(1)证明:∵等腰△ABC中,AB=BC,∠A=30°将△ABC绕点B顺时针旋转30°,得△A1BC1,
∴AB=BC1=A1B=BC,∠ABE=∠C1BF,∠A=∠C1=∠A1=∠C,
在△ABE和△C1BF中,
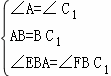 ,
,
∴△ABE≌△C1BF(ASA);
(2)证明:∵△ABE≌△C1BF,
∴EB=BF.
又∵A1B=CB,
∴A1B﹣EB=CB﹣BF,
∴EA1=FC;
(3)答:四边形ABC1D是菱形.
证明:∵∠A1=∠C=30°,∠ABA1=∠CBC1=30°,
∠A1=∠C=∠ABA1=∠CBC1.
∴AB∥C1D,AD∥BC1,
∴四边形ABC1D是平行四边形
∵AB=BC1,
∴四边形ABC1D是菱形.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 4
4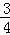 )﹣2+
)﹣2+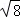 ﹣2sin45°﹣|1﹣
﹣2sin45°﹣|1﹣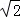 |.
|.

 D.
D. 
 度是5℃,该电冰箱冷藏室的温度比冷冻室的温度高 ℃.
度是5℃,该电冰箱冷藏室的温度比冷冻室的温度高 ℃. +
+ ×
× )×
)× 之值为何?( )
之值为何?( ) B.12
B.12 C.12
C.12 D. 18
D. 18