Question

【题目】如图，AB是圆O的直径，弦CD⊥AB，∠BCD=30°，CD=4 ，则S阴影=（ ）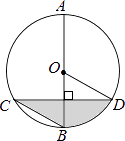
A.2π??
B. π??
C. π??
D. π

Answer 1

【答案】B
【解析】解：如图，假设线段CD、AB交于点E，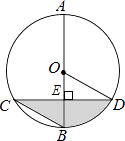
∵AB是⊙O的直径，弦CD⊥AB，
∴CE=ED=2 ，
又∵∠BCD=30°，
∴∠DOE=2∠BCD=60°，∠ODE=30°，
∴OE=DEcot60°=2 × =2，OD=2OE=4，
∴S阴影=S扇形ODB﹣S△DOE+S△BEC= ﹣ OE×DE+ BECE= ﹣2 +2 = ．
故选B．
【考点精析】本题主要考查了垂径定理和圆周角定理的相关知识点，需要掌握垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题．