Question

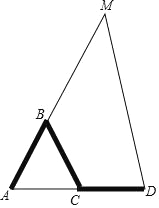
【题目】如图，AB﹣BC﹣CD是一根三节棍，其中线段AB、BC、CD首尾顺次相连，且AB＝BC＝CD，将这个三节棍摆放在△AMD中，使它的两个端点与△AMD两个顶点重合，三节棍的首尾两节在△AMD的边上，则AB﹣BC﹣CD就是△AMD的配套三节棍．

（1）若∠A＝60°，AD＝60，求△AMD的配套三节棍的总长；

（2）若AM＝AD，△AMD的配套三节棍AB﹣BC﹣CD中一边BC平行于MD，利用直尺圆规画出图形，并求出∠A的度数．（保留作图痕迹）

Answer 1

【答案】（1）90；（2）作图见解析；∠A＝60°.

【解析】

（1）根据已知条件即可得到结论；

（2）根据等腰三角形的性质得到∠M=∠D，∠A=∠BCA，由平行线的性质得到∠BCA=∠D，等量代换得到∠A=∠D=∠M，于是得到结论．

（1）∵∠A＝60°，AB＝BC，AB＝BC＝CA，

∵AD＝60，

∴AB＝BC＝CA＝CD＝30，

∴△AMD的配套三节棍的总长为3×30＝90；

（2）①作射线AE，在射线AE上截取AB＝BM，

②分别以A，M为圆心，AM的长为半径画弧，两弧交于点D，

③连接AD，MD，

④过B作BC∥DM交AD于D，

则图形即为所求；

证明：∵AM＝AD，

∴∠M＝∠D，

∵AB＝BC，

∴∠A＝∠BCA，

∵BC∥MD，

∴∠BCA＝∠D，

∴∠A＝∠D＝∠M，

∵∠A+∠D+∠M＝180°，

∴∠A＝60°，