题目内容
 如图,AB=AC,AB⊥AC,BD平分∠ABC,过C点作CE⊥BD于E,交BA延长线于F,则下列结论中错误的是
如图,AB=AC,AB⊥AC,BD平分∠ABC,过C点作CE⊥BD于E,交BA延长线于F,则下列结论中错误的是
- A.△BEC≌△BEF
- B.△ABD≌△ACF
- C.CD=2DE
- D.BD=2CE
C
分析:根据已知条件,易证△BEC≌△BEF,所以BF=BC,所以∠F=∠BCE,根据等腰三角形三线合一这一性质,CE=FE,再证明△ABD≌△ACF,证得BD=CF,从而证得BD=2CE.
解答:∵BD平分∠ABC
∴∠FBE=∠CBE
∵BE⊥CF
∴∠BEF=∠BEC
又∵BE=BE
∴△BEC≌△BEF,故A正确;
∴CE=EF
∴CF=2CE
∵∠ABD+∠ADB=90°,∠ABD+∠AFE=90°
∴∠ADB=∠BFE
又∵AB=AC,∠BAD=∠CAF=90°,
∴△ABD≌△ACF,故B正确;
∴BD=CF=2CE,故D正确.
故选C.
点评:此题主要考查了角平分线的性质及全等三角形的判定,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.三角形全等的证明是正确解答本题的关键.
分析:根据已知条件,易证△BEC≌△BEF,所以BF=BC,所以∠F=∠BCE,根据等腰三角形三线合一这一性质,CE=FE,再证明△ABD≌△ACF,证得BD=CF,从而证得BD=2CE.
解答:∵BD平分∠ABC
∴∠FBE=∠CBE
∵BE⊥CF
∴∠BEF=∠BEC
又∵BE=BE
∴△BEC≌△BEF,故A正确;
∴CE=EF
∴CF=2CE
∵∠ABD+∠ADB=90°,∠ABD+∠AFE=90°
∴∠ADB=∠BFE
又∵AB=AC,∠BAD=∠CAF=90°,
∴△ABD≌△ACF,故B正确;
∴BD=CF=2CE,故D正确.
故选C.
点评:此题主要考查了角平分线的性质及全等三角形的判定,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.三角形全等的证明是正确解答本题的关键.

练习册系列答案
相关题目
 24、如图,AB=AC=AD.
24、如图,AB=AC=AD. (2012•虹口区一模)已知:如图,AB=AC,∠DAE=∠B.
(2012•虹口区一模)已知:如图,AB=AC,∠DAE=∠B.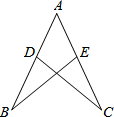 (2013•来宾)如图,AB=AC,D,E分别是AB,AC上的点,下列条件中不能证明△ABE≌△ACD的是
(2013•来宾)如图,AB=AC,D,E分别是AB,AC上的点,下列条件中不能证明△ABE≌△ACD的是 如图,AB=AC,∠C=67°,AB的垂直平分线EF交AC于点D,求∠DBC的度数.
如图,AB=AC,∠C=67°,AB的垂直平分线EF交AC于点D,求∠DBC的度数. 如图,AB=AC=10,∠A=40°,AB的垂直平分线MN交AC于点D,求:
如图,AB=AC=10,∠A=40°,AB的垂直平分线MN交AC于点D,求: