��Ŀ����
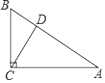
����Ŀ����ͼ1���ڳ�����![]() �У�BC=3������
��BC=3������![]() ��
��![]() ��������ÿ��1����λ���ٶȣ�������
��������ÿ��1����λ���ٶȣ�������![]() �����ƶ�����
�����ƶ�����![]() ����ֱ��
����ֱ��![]() �ĶԳ�
�ĶԳ�![]() �����
�����![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ![]()
��1����P�����߶�BC���Ҳ���C���غ�ʱ����ֱ��PB����ֱ��CD�ཻ�ڵ�M���ҡ�PAM=45��������AB�ij�
��2����AB=4
����ͼ2������B������AC��ʱ����Ȼ��PCB����ֱ�������Σ����ʱt��ֵ
���Ƿ��������ͼ2��ʱ�̣�ʹ����PCB����ֱ�������Σ������ڣ���ֱ��д�����з��������t��ֵ���������ڣ���˵������

���𰸡���1��AB�ij�Ϊ3����2����![]() ����t��ֵΪ
����t��ֵΪ![]() ��
��![]() ��4.
��4.
��������
��1����ͼ��ʾ���ӳ�![]() ��CD����M������AM���ýǽDZ�֤��
��CD����M������AM���ýǽDZ�֤��![]() �����Ƴ�AB=BC=3.
�����Ƴ�AB=BC=3.
��2������Rt��![]() �У��ҳ��߳����ù��ɶ�������������⣻
�У��ҳ��߳����ù��ɶ�������������⣻
�ڷ�����������ۣ�![]() ��
��![]() ��
��![]() ���ֱ�������Ӧ��ͼ�Σ���
���ֱ�������Ӧ��ͼ�Σ���![]() �У��ֱ��ҳ��߳������ù��ɶ��������������.
�У��ֱ��ҳ��߳������ù��ɶ��������������.
��1����ͼ��ʾ���ӳ�![]() ��CD����M������AM��
��CD����M������AM��

���۵������ʿ�֪![]() ��
��![]() ��
��![]()
��![]() ��
��![]() ��
��
��![]()
��![]() ��
��![]() ��
�У�

��![]() ��
��![]() ��AAS��
��AAS��
��![]()
����ABCD������AD=BC=3��
��AB=3
��2������Rt��ABC��![]()
�ߵ�P����˶�ʱ��Ϊt���ٶ�Ϊ1����BP=t��
![]() ��
��![]() ��
��![]() ,
,
��Rt��![]() �У��ɹ��ɶ�����
�У��ɹ��ɶ�����![]() ����
����![]() �����
�����![]() .
.
�ڵ�![]() ������ͼ��ʾ��
������ͼ��ʾ��

���ı���ABCDΪ���Σ���AD=BC=3��CD=AB=4��
���۵�������![]() ����Rt��
����Rt��![]() ��
�У�
![]() ��
��
��![]()
��Rt��![]() ��
��![]() ��
��![]()
![]() ����
����![]() �����
�����![]()
����![]() =90��ʱ������ͼ��ʾ��
=90��ʱ������ͼ��ʾ��

���۵��ɵ�![]() ��
��
��Rt��![]() ��
�У�![]()
��Rt��![]() ��
��![]() ��
��![]() ��
��![]()
![]() ����
����![]() �����
�����![]()
��![]() =90��ʱ������ͼ��ʾ�������۵����ı���
=90��ʱ������ͼ��ʾ�������۵����ı���![]() Ϊ�����Σ���PB=AB=4
��������PB=AB=4

���ϣ����������t��ֵΪ![]() ��
��![]() ��4.
��4.

 ���ɿ��õ�Ԫ����AB��ϵ�д�
���ɿ��õ�Ԫ����AB��ϵ�д� С�����ϵ�д�
С�����ϵ�д�