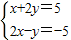题目内容
（2009•通州区二模）已知二次函数y=x2-3x-4．（1）用配方法求这个二次函数图象的顶点坐标和对称轴；
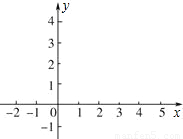
（2）画出这个函数的大致图象，指出函数值不小于0时x的取值范围．
【答案】分析：（1）当二次项系数为1，用配方法时，应注意配上“一次项系数一半的平方”；
（2）画函数图象，应该明确抛物线的顶点坐标，对称轴，与x轴（y轴）的交点，再根据图形求函数值不小于0时，即y≥0时，x的取值范围．
解答：
解：（1）∵y=x2-3x-4
=x2-3x+（
）2-（
）2-4
=（x-
）2-
；
∴二次函数图象的顶点坐标是（
，-
），
对称轴方程是x=
．
（2）∵y=x2-3x-4=（x+1）（x-4），
图象与x轴两交点坐标为（-1，0），（4，0），
∴函数值不小于0时，x的取值范围是x≤-1或x≥4．
图象如图．
点评：本题主要考查了配方法确定二次函数的顶点及对称轴，在配方的过程中注意要保持式子的值不变．
（2）画函数图象，应该明确抛物线的顶点坐标，对称轴，与x轴（y轴）的交点，再根据图形求函数值不小于0时，即y≥0时，x的取值范围．
解答：
解：（1）∵y=x2-3x-4=x2-3x+（
）2-（）2-4=（x-
）2-；∴二次函数图象的顶点坐标是（
，-），对称轴方程是x=
．（2）∵y=x2-3x-4=（x+1）（x-4），
图象与x轴两交点坐标为（-1，0），（4，0），
∴函数值不小于0时，x的取值范围是x≤-1或x≥4．
图象如图．
点评：本题主要考查了配方法确定二次函数的顶点及对称轴，在配方的过程中注意要保持式子的值不变．
练习册系列答案
阅读快车系列答案
相关题目
=c+
的解是x1=c，x2=
；
=c-
（即x+
=c+
）的解是x1=c，x2=-
；x+
=c+
的解是：x1=c，x2=
，…
=c+
（m≠0）的解，并利用“方程的解”的概念进行验证；
=a+
的解吗？若能，请求出此方程的解；若不能，请说明理由．
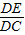的值．
