ƒøƒ⁄»ð
°æƒø°ø»Áπ˚“ª∏ˆÀƒ±þ–Œµƒ∂‘Ω«œþ∞—Àƒ±þ–Œ∑÷≥…¡Ω∏ˆ»˝Ω«–Œ£¨“ª∏ˆ «µ»±þ»˝Ω«–Œ£¨¡Ì“ª∏ˆ «∏√∂‘Ω«œþÀ˘∂‘µƒΩ«Œ™![]() µƒ»˝Ω«–Œ£¨Œ“√«∞—’‚Ãı∂‘Ω«œþΩ–◊ˆ’‚∏ˆÀƒ±þ–Œµƒ¿ÌœÎ∂‘Ω«œþ£¨’‚∏ˆÀƒ±þ–Œ≥∆Œ™¿ÌœÎÀƒ±þ–Œ£Æ
µƒ»˝Ω«–Œ£¨Œ“√«∞—’‚Ãı∂‘Ω«œþΩ–◊ˆ’‚∏ˆÀƒ±þ–Œµƒ¿ÌœÎ∂‘Ω«œþ£¨’‚∏ˆÀƒ±þ–Œ≥∆Œ™¿ÌœÎÀƒ±þ–Œ£Æ
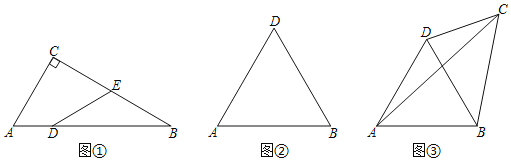
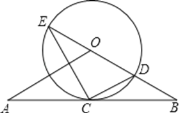
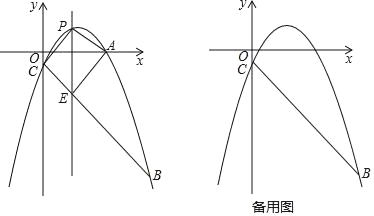
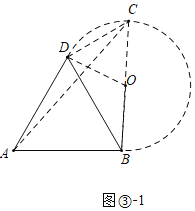
£®1£©»ÁÕº¢Ÿ£¨‘⁄![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() Œ™
Œ™![]() …œ“ªµ„£¨
…œ“ªµ„£¨![]() £¨
£¨![]() Œ™
Œ™![]() ÷–µ„£¨¡¨Ω”
÷–µ„£¨¡¨Ω”![]() £¨«Û÷§£∫Àƒ±þ–Œ
£¨«Û÷§£∫Àƒ±þ–Œ![]() Œ™¿ÌœÎÀƒ±þ–Œ£ª
Œ™¿ÌœÎÀƒ±þ–Œ£ª
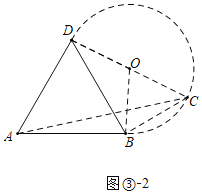
£®2£©»ÁÕº¢⁄£¨![]() «µ»±þ»˝Ω«–Œ£¨»Ù
«µ»±þ»˝Ω«–Œ£¨»Ù![]() Œ™¿ÌœÎ∂‘Ω«œþ£¨Àƒ±þ–Œ
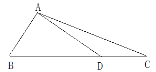
Œ™¿ÌœÎ∂‘Ω«œþ£¨Àƒ±þ–Œ![]() Œ™¿ÌœÎÀƒ±þ–Œ£Æ«Îª≠Õº’“≥ˆ∑˚∫œÃıº˛µƒCµ„¬‰‘⁄‘ı—˘µƒÕº–Œ…œ£ª(‘⁄Õº÷–±Í≥ˆ±ÿ“™µƒ ˝æð)
Œ™¿ÌœÎÀƒ±þ–Œ£Æ«Îª≠Õº’“≥ˆ∑˚∫œÃıº˛µƒCµ„¬‰‘⁄‘ı—˘µƒÕº–Œ…œ£ª(‘⁄Õº÷–±Í≥ˆ±ÿ“™µƒ ˝æð)
£®3£©‘⁄£®2£©µƒÃıº˛œ¬£¨
¢Ÿ»Ù![]() Œ™÷±Ω«»˝Ω«–Œ£¨
Œ™÷±Ω«»˝Ω«–Œ£¨![]() £¨«Û
£¨«Û![]() µƒ≥§∂»£ª
µƒ≥§∂»£ª
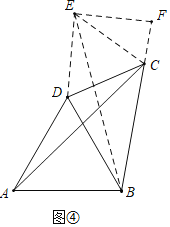
¢⁄»ÁÕº¢€£¨»Ù![]() £¨
£¨![]() £¨
£¨![]() £¨«Î÷±Ω”–¥≥ˆ
£¨«Î÷±Ω”–¥≥ˆ![]() °¢
°¢![]() °¢
°¢![]() ÷ƺ‰µƒ ˝¡øπÿœµ£Æ
÷ƺ‰µƒ ˝¡øπÿœµ£Æ
°æ¥∞∏°ø£®1£©œÍº˚Ω‚Œˆ£ª£®2£©œÍº˚Ω‚Œˆ£ª£®3£©¢Ÿ![]() ªÚ
ªÚ![]() £ª ¢⁄
£ª ¢⁄![]()
°æΩ‚Œˆ°ø
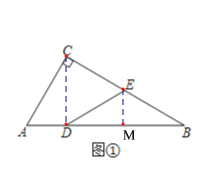
£®1£©¡¨Ω”CD£¨π˝µ„E◊˜EM°ÕAB£¨“◊÷§EM «BDµƒ÷–¥πœþ£¨µ√°œEDB=°œB=30°„£¨¥”∂¯µ√°œCED=60°„£¨Ω¯∂¯µ√![]() «µ»±þ»˝Ω«–Œ£¨º¥ø…µ√µΩΩ·¬€£ª
«µ»±þ»˝Ω«–Œ£¨º¥ø…µ√µΩΩ·¬€£ª
£®2£©◊˜µ»—¸»˝Ω«–ŒODB£¨ πµ√OD£ΩOB£¨°œDOB£Ω120°„£¨“‘OŒ™‘≤–ƒ£¨ODŒ™∞Îæ∂◊˜°—O£¨µ±µ„C‘⁄ª°BCD…œ ±£¨¬˙◊„Ãıº˛£ª
£®3£©¢Ÿ»Ù![]() Œ™÷±Ω«»˝Ω«–Œ£¨∑÷¡Ω÷÷«ÈøˆÃ÷¬€£∫£®i£©µ±°œBDC=90°„ ±£ª£®ii£©µ±°œDBC=90°„ ±£¨∑÷±«Û≥ˆ¥∞∏º¥ø…£ª¢⁄Ω´
Œ™÷±Ω«»˝Ω«–Œ£¨∑÷¡Ω÷÷«ÈøˆÃ÷¬€£∫£®i£©µ±°œBDC=90°„ ±£ª£®ii£©µ±°œDBC=90°„ ±£¨∑÷±«Û≥ˆ¥∞∏º¥ø…£ª¢⁄Ω´![]() »∆µ„DƒÊ ±’Ζ˝◊™60°„£¨µ√µΩ
»∆µ„DƒÊ ±’Ζ˝◊™60°„£¨µ√µΩ![]() £¨¡¨Ω”EC£¨π˝µ„E◊˜EF°ÕBC£¨ΩªBCµƒ—”≥§œþ”⁄µ„F£¨ø…µ√
£¨¡¨Ω”EC£¨π˝µ„E◊˜EF°ÕBC£¨ΩªBCµƒ—”≥§œþ”⁄µ„F£¨ø…µ√![]() «µ»±þ»˝Ω«–Œ£¨”√∫¨x£¨yµƒ¥˙ ˝ Ω±Ì æEF£¨CF£¨Ω¯∂¯µ√µΩBFµƒ±Ì¥Ô Ω£¨¿˚”√π¥π…∂®¿Ì£¨º¥ø…µ√µΩΩ·¬€£Æ
«µ»±þ»˝Ω«–Œ£¨”√∫¨x£¨yµƒ¥˙ ˝ Ω±Ì æEF£¨CF£¨Ω¯∂¯µ√µΩBFµƒ±Ì¥Ô Ω£¨¿˚”√π¥π…∂®¿Ì£¨º¥ø…µ√µΩΩ·¬€£Æ
£®1£©¡¨Ω”CD£¨π˝µ„E◊˜EM°ÕAB£¨»ÁÕº¢Ÿ£¨
°þ‘⁄![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨
°ýAB=4£¨BC=![]() £¨BD=4-1=3£¨
£¨BD=4-1=3£¨
°þ![]() Œ™
Œ™![]() ÷–µ„£¨
÷–µ„£¨
°ýBE=![]() £¨
£¨
°þ‘⁄![]() ÷–£¨°œB=30°„£¨EM°ÕAB£¨
÷–£¨°œB=30°„£¨EM°ÕAB£¨
°ýBM=BEcos30°„=![]() £¨
£¨
°ýDM=BM=![]() £¨º¥EM «BDµƒ÷–¥πœþ£¨
£¨º¥EM «BDµƒ÷–¥πœþ£¨
°ýED=EB=EC£¨
°ý°œEDB=°œB=30°„£¨
°ý°œCED=60°„£¨
°ý![]() «µ»±þ»˝Ω«–Œ£¨
«µ»±þ»˝Ω«–Œ£¨
”÷°þ°œA=180°„-°œB-°œACB=60°„£¨
°ýÀƒ±þ–Œ![]() Œ™¿ÌœÎÀƒ±þ–Œ£ª
Œ™¿ÌœÎÀƒ±þ–Œ£ª
£®2£©»ÁÕº¢⁄÷–£¨◊˜µ»—¸»˝Ω«–ŒODB£¨ πµ√OD£ΩOB£¨°œDOB£Ω120°„£¨“‘OŒ™‘≤–ƒ£¨ODŒ™∞Îæ∂◊˜°—O£¨µ±µ„C‘⁄ª°BCD…œ ±£¨°œDCB£Ω![]() °œDOB£Ω60°„£¨¬˙◊„Ãıº˛£ª
°œDOB£Ω60°„£¨¬˙◊„Ãıº˛£ª
£®3£©¢Ÿ»Ù![]() Œ™÷±Ω«»˝Ω«–Œ£¨∑÷¡Ω÷÷«ÈøˆÃ÷¬€£∫
Œ™÷±Ω«»˝Ω«–Œ£¨∑÷¡Ω÷÷«ÈøˆÃ÷¬€£∫
£®i£©µ±°œBDC=90°„ ±£¨»ÁÕº¢€-1£¨
°þ°œBCD=60°„£¨BC=2£¨
°ý°œDBC=30°„£¨BD=BC![]() cos30°„=
cos30°„=![]() £¨
£¨
°þ![]() «µ»±þ»˝Ω«–Œ£¨
«µ»±þ»˝Ω«–Œ£¨
°ýAB=BD=![]() £¨°œABD=60°„£¨
£¨°œABD=60°„£¨
°ý°œABC=90°„£¨
°ý![]() £ª
£ª
£®ii£©µ±°œDBC=90°„ ±£¨»ÁÕº¢€-2£¨
Õ¨¿Ìø…µ√£∫°œADC=90°„£¨DC=4£¨AD=![]() £¨
£¨
°ý![]() £Æ
£Æ
◊€…œÀ˘ ˆ£∫AC=![]() ªÚ
ªÚ![]() £ª
£ª
¢⁄Ω´![]() »∆µ„DƒÊ ±’Ζ˝◊™60°„£¨µ√µΩ
»∆µ„DƒÊ ±’Ζ˝◊™60°„£¨µ√µΩ![]() £¨¡¨Ω”EC£¨π˝µ„E◊˜EF°ÕBC£¨ΩªBCµƒ—”≥§œþ”⁄µ„F£¨»ÁÕº¢Ð£¨
£¨¡¨Ω”EC£¨π˝µ„E◊˜EF°ÕBC£¨ΩªBCµƒ—”≥§œþ”⁄µ„F£¨»ÁÕº¢Ð£¨
°ý°œCDE=60°„£¨ED=CD£¨BE=AC=z£¨
°ý![]() «µ»±þ»˝Ω«–Œ£¨
«µ»±þ»˝Ω«–Œ£¨
°ýEC=CD=x£¨°œDCE=60°„£¨
°þ°œBCD=60°„£¨
°ý°œECF=180°„-60°„-60°„=60°„£¨
°ýEF=EC![]() sin60°„=
sin60°„=![]() £¨CF= EC
£¨CF= EC![]() cos60°„=
cos60°„=![]() £¨
£¨
°ýBF=BC+CF=y+![]() £¨
£¨
°ýBE=![]() =
=![]() £¨
£¨
°ýz=![]() £¨º¥£∫
£¨º¥£∫![]() £Æ
£Æ


 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
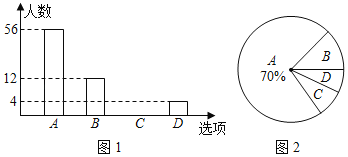
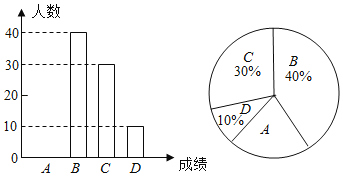
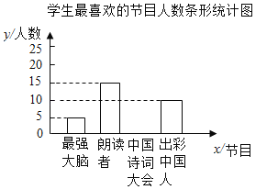
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏°æƒø°øŒ™¡ÀΩ‚ƒ≥–£—ß…˙∂‘°∂◊Ó«ø¥Ûƒ‘°∑°¢°∂¿ ∂¡’þ°∑°¢°∂÷–π˙ ´¥ ¥Ûª·°∑°¢°∂≥ˆ≤ ÷–π˙»À°∑Àƒ∏ˆµÁ ”Ω⁄ƒøµƒœ≤∞Æ«Èøˆ£¨ÀÊñi≥È»°¡À![]() √˚—ß…˙Ω¯––µ˜≤ÈÕ≥º∆£®“™«Û√ø√˚—ß…˙—°≥ˆ≤¢«“÷ªƒÐ—°≥ˆ“ª∏ˆ◊‘º∫◊Óœ≤∞ƵƒΩ⁄ƒø£©£¨≤¢Ω´µ˜≤ÈΩ·π˚ªÊ÷∆≥…»ÁÕºÕ≥º∆Õº±Ì£∫
√˚—ß…˙Ω¯––µ˜≤ÈÕ≥º∆£®“™«Û√ø√˚—ß…˙—°≥ˆ≤¢«“÷ªƒÐ—°≥ˆ“ª∏ˆ◊‘º∫◊Óœ≤∞ƵƒΩ⁄ƒø£©£¨≤¢Ω´µ˜≤ÈΩ·π˚ªÊ÷∆≥…»ÁÕºÕ≥º∆Õº±Ì£∫
—ß…˙◊Óœ≤∞ƵƒΩ⁄ƒø»À ˝Õ≥º∆±Ì
Ω⁄ƒø | »À ˝£®√˚£© | ∞Ÿ∑÷±» |
◊Ó«ø¥Ûƒ‘ | 5 | 10% |
¿ ∂¡’þ | 15 | |
÷–π˙ ´¥ ¥Ûª· |
| 40% |
≥ˆ≤ ÷–π˙»À | 10 | 20% |
∏˘æð“‘…œ–≈œ¢£¨ªÿ¥œ¬¡–Œ £∫
£®1£©![]() °°£¨
°°£¨![]() °°£ª
°°£ª
£®2£©≤π»´…œ√ʵƒÃı–ŒÕ≥º∆Õº£ª
£®3£©»Ù∏√–£π≤”–—ß…˙![]() √˚£¨π¿º∆∏√–£—ß…˙◊Óœ≤∞Æ°∂¿ ∂¡’þ°∑Ω⁄ƒøµƒ»À ˝£Æ
√˚£¨π¿º∆∏√–£—ß…˙◊Óœ≤∞Æ°∂¿ ∂¡’þ°∑Ω⁄ƒøµƒ»À ˝£Æ