题目内容
 如图,已知反比例函数
如图,已知反比例函数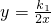 的图象与一次函数y=k2x+b的图象交于A,B两点,A(1,n),B(
的图象与一次函数y=k2x+b的图象交于A,B两点,A(1,n),B( ,-2),请你在x轴上找点P,使△AOP为等腰三角形,则这样的点P有________个,其坐标分别是________.
,-2),请你在x轴上找点P,使△AOP为等腰三角形,则这样的点P有________个,其坐标分别是________.
4 ( ,0),(-
,0),(- ,0),(1,0),(2,0)
,0),(1,0),(2,0)
分析:将点B的坐标代入反比例函数解析式,得出k的值,将点A的横坐标代入,得出点A的坐标,求出OA的长度,分情况讨论:①OA=OP,②AO=AP,③PO=PA;分别得到点P的坐标即可.
解答:将点B(- ,-2),代入反比例函数
,-2),代入反比例函数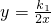 ,可得:-2=
,可得:-2= ,
,
解得:k1=2,
∴反比例函数解析式为:y= ,
,
将点A的横坐标x=1代入y= ,可得y=1,
,可得y=1,
故点A的坐标为(1,1),
则OA= ,
,
①若OA=OP,如图①所示:

此时可得P1( ,0),P2(-
,0),P2(- ,0);
,0);
②若AO=AP,如图②所示:

此时可得P3(2,0);
③若PO=PA,如图③所示:
 ,
,
此时△OAP4是等腰直角三角形,P4(1,0).
综上可得点P的坐标为:( ,0)或(-
,0)或(- ,0)或(1,0)或(2,0),共4个.
,0)或(1,0)或(2,0),共4个.
故答案为:4、( ,0),(-
,0),(- ,0),(1,0),(2,0).
,0),(1,0),(2,0).
点评:本题考查了反比例函数的综合,涉及了待定系数法求反比例函数解析式、反比例函数图象上点的坐标特征及等腰三角形的判定,解答本题的关键是数形结合思想及分类讨论思想的综合运用.
 ,0),(-
,0),(- ,0),(1,0),(2,0)
,0),(1,0),(2,0)分析:将点B的坐标代入反比例函数解析式,得出k的值,将点A的横坐标代入,得出点A的坐标,求出OA的长度,分情况讨论:①OA=OP,②AO=AP,③PO=PA;分别得到点P的坐标即可.
解答:将点B(-
 ,-2),代入反比例函数
,-2),代入反比例函数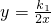 ,可得:-2=
,可得:-2= ,
,解得:k1=2,
∴反比例函数解析式为:y=
 ,
,将点A的横坐标x=1代入y=
 ,可得y=1,
,可得y=1,故点A的坐标为(1,1),
则OA=
 ,
,①若OA=OP,如图①所示:

此时可得P1(
 ,0),P2(-
,0),P2(- ,0);
,0);②若AO=AP,如图②所示:

此时可得P3(2,0);
③若PO=PA,如图③所示:
 ,
,此时△OAP4是等腰直角三角形,P4(1,0).
综上可得点P的坐标为:(
 ,0)或(-
,0)或(- ,0)或(1,0)或(2,0),共4个.
,0)或(1,0)或(2,0),共4个.故答案为:4、(
 ,0),(-
,0),(- ,0),(1,0),(2,0).
,0),(1,0),(2,0).点评:本题考查了反比例函数的综合,涉及了待定系数法求反比例函数解析式、反比例函数图象上点的坐标特征及等腰三角形的判定,解答本题的关键是数形结合思想及分类讨论思想的综合运用.

练习册系列答案
相关题目
 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数y=
如图,已知反比例函数y= 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数y=
如图,已知反比例函数y=