题目内容

18．已知a和b互为相反数，且满足（a+3）2-（b+3）2=18，a2•b3=-$\frac{243}{32}$．

分析 由a和b互为相反数，得出a+b=0，a=-b，进一步利用平方差公式因式分解，代入求得a、b的数值，进一步代入求得结果即可．

解答 解：∵a和b互为相反数，
∴a+b=0，a=-b，
∵（a+3）2-（b+3）2=18，
∴（a+3+b+3）（a+3-b-3）=18，
∴6（a-b）=18，
即12a=18，
解得：a=$\frac{3}{2}$，
∴b=-$\frac{3}{2}$，
∴a2•b3=$\frac{9}{4}$×（-$\frac{27}{8}$）=-$\frac{243}{32}$．
故答案为：-$\frac{243}{32}$．

点评 此题考查因式分解的实际运用，相反数的意义，掌握平方差公式因式分解是解决问题的关键．

练习册系列答案
相关题目
4．一群鸽子，飞过一棵高高的树，一部分鸽子落在树上，其他的停在树下，一只落在树上的鸽子对树下的鸽子说：“倘若你们当中有一只飞上来，你们的数目就是我们总数的三分之一；倘若我们中飞下去一只，我们的数目恰好与你们相同！”猜一猜，有多少只鸽子在树上，多少只鸽子在树下？
5．甲、乙两地相距324千米，一列慢车从甲站开出，每小时行驶72千米，另一列快车从乙站开出，每小时行驶90千米．
（1）两列车同时开出，相向而行，几小时后相遇？
（2）两列车同时开出，同向而行，快车在慢车后面，快车开出几小时后追上慢车？
6．如图1，点B的坐标为（-1，0），点C的坐标为（3，0），点D的坐标为（0，3），抛物线的经过B，C，D三点，且顶点为A．
（1）求抛物线的解析式和点A的坐标；
（2）如图2，平行于x轴的直线y=m（0＜m＜4）分别于AO、AC交于点E和F，若将△AEF沿EF折叠，设折叠后的△A′EF与△AOC重叠部分的面积为S．
①用含m的代数式表示线段EF的长；
②试求S与m的函数关系式及m的取值范围．
（3）请在直线BD上找一点M，使△ACM的周长最小，求出M点的坐标．
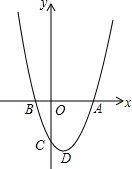13．如图，已知抛物线y=ax2-2ax-b（a＞0）与x轴的一个交点为B（-1，0），与y轴的负半轴交于点C，顶点为D．
（1）直接写出抛物线的对称轴，及抛物线与x轴的另一个交点A的坐标；
（2）若以AD为直径的圆经过点C，求抛物线的解析式；
（3）在（2）的条件下，若点E在抛物线的对称轴上，抛物线上是否存在点F，使以A，B，E，F为顶点的四边形为平行四边形？若存在，求出所有满足条件的点F的坐标；若不存在，请说明理由．
3．多项式x2-9因式分解的结果是（x+3）（x-3）．
10．已知△ABC中，∠ABC=∠ACB，D为射线CB上一点（不与C、B重合），点E为射线CA上一点，∠ADE=∠AED．设∠BAD=α，∠CDE=β．
（1）如图（1），
①若∠BAC=40°，∠DAE=30°，则α=10°，β=5°．
②写出α与β的数量关系，并说明理由；
（2）如图（2），当D点在BC边上，E点在CA的延长线上时，其它条件不变，写出α与β的数量关系，并说明理由．
（3）如图（3），D在CB的延长线上，根据已知补全图形，并直接写出α与β的关系式$β=\frac{180°-α}{2}$．
7．通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的．下面是一个案例，请补充完整．
原题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，则EF=BE+DF，试说明理由．

（1）思路梳理
∵AB=AD，
∴把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合．
∵∠ADC=∠B=90°，
∴∠FDG=180°，点F、D、G共线．
根据SAS，易证△AFG≌△AFE，得EF=BE+DF．
（2）类比引申
如图2，四边形ABCD中，AB=AD，∠BAD=90°点E、F分别在边BC、CD上，∠EAF=45°．若∠B、∠D都不是直角，则当∠B与∠D满足等量关系∠B+∠ADC=180°时，仍有EF=BE+DF．
（3）联想拓展
如图3，在△ABC中，∠BAC=90°，AB=AC，点D、E均在边BC上，且∠DAE=45°．猜想BD、DE、EC应满足的等量关系，并写出推理过程．
8．如图，⊙O的半径为5，直线l是⊙O的切线，A为切点，则点O到直线l的距离是（　　）
A．2.5B．3C．5D．10

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网