题目内容
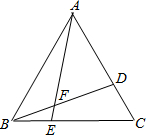 已知△ABC是等边三角形,点D、E分别在AC、BC上,且CD=BE,则∠AFD=________.
已知△ABC是等边三角形,点D、E分别在AC、BC上,且CD=BE,则∠AFD=________.
60°
分析:根据等边三角形性质得出∠ABE=∠C=60°,AB=BC,证△ABE≌△BCD,推出∠BAE=∠CBD,求出∠AFD=∠ABF+∠BAE=∠ABF+∠CBD=∠ABC,代入求出即可.
解答:∵△ABC是等边三角形,
∴∠ABE=∠C=60°,AB=BC,
在△ABE和△BCD中
 ,
,
∴△ABE≌△BCD(SAS),
∴∠BAE=∠CBD,
∴∠AFD=∠ABF+∠BAE=∠ABF+∠CBD=∠ABC=60°,
或答案为:60°.
点评:本题考查了等边三角形的性质,全等三角形的性质和判定,三角形的外角性质的应用.
分析:根据等边三角形性质得出∠ABE=∠C=60°,AB=BC,证△ABE≌△BCD,推出∠BAE=∠CBD,求出∠AFD=∠ABF+∠BAE=∠ABF+∠CBD=∠ABC,代入求出即可.
解答:∵△ABC是等边三角形,
∴∠ABE=∠C=60°,AB=BC,
在△ABE和△BCD中
 ,
,∴△ABE≌△BCD(SAS),
∴∠BAE=∠CBD,
∴∠AFD=∠ABF+∠BAE=∠ABF+∠CBD=∠ABC=60°,
或答案为:60°.
点评:本题考查了等边三角形的性质,全等三角形的性质和判定,三角形的外角性质的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
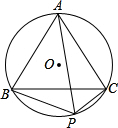 已知△ABC是等边三角形,⊙O为它的外接圆,点P是
已知△ABC是等边三角形,⊙O为它的外接圆,点P是
 已知D是等边△ABC外一点,∠BDC=120°,则AD、BD、DC三条线段的数量关系为
已知D是等边△ABC外一点,∠BDC=120°,则AD、BD、DC三条线段的数量关系为
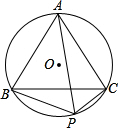 已知△ABC是等边三角形,⊙O为它的外接圆,点P是
已知△ABC是等边三角形,⊙O为它的外接圆,点P是 上任一点.
上任一点. 上任一点.
上任一点.