题目内容
9.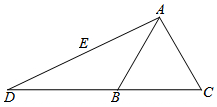 如图,延长等边三角形ABC一边CB到D,连接AD.以A为圆心,AC为半径画弧交AD于E.已知AC=2,∠D=20°,求DE的长(精确到0.1).(参考数据:$\sqrt{3}$≈1.73,tan20°≈0.36,sin20°≈0.34,cos20°≈0.94)
如图,延长等边三角形ABC一边CB到D,连接AD.以A为圆心,AC为半径画弧交AD于E.已知AC=2,∠D=20°,求DE的长(精确到0.1).(参考数据:$\sqrt{3}$≈1.73,tan20°≈0.36,sin20°≈0.34,cos20°≈0.94)
分析 过A作AF⊥BC,交点为F,根据三角函数的定义得出AF的长,再由△ADF中,根据∠D=20°,即可得出AD从而得出DE即可.
解答  解:如图,过A作AF⊥BC,交点为F,
解:如图,过A作AF⊥BC,交点为F,
∵△ABC为等边三角形,
∴AB=BC=AC=2,∠ABC=60°.
在△ABF中,sin∠ABC=$\frac{AF}{AB}$,
∵∠ABC=60°,AB=2,
∴sin60°=$\frac{AF}{2}$,即$\frac{\sqrt{3}}{2}$=$\frac{AF}{2}$,
∴AF=$\sqrt{3}$,
在△ADF中,sinD=$\frac{AF}{AD}$,
∵∠D=20°,AF=$\sqrt{3}$,
∴sin20°=$\frac{AF}{\sqrt{3}}$,即$\frac{\sqrt{3}}{AD}$≈0.34,
∴AD≈5.1,
由题知,
∴AE=AC=2,
∴DE=3.1.
点评 本题考查了解直角三角形,熟练应用三角函数的定义是解题的关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
1.如图所示,某公园设计节日鲜花摆放方案,其中一个花坛由一批花盆堆成六角垛,顶层一个,以下各层堆成六边形,逐层每边增加一个花盆,若这垛花盆底层最长的一排共有13个花盆,则底层的花盆的个数是( )


| A. | 91 | B. | 127 | C. | 169 | D. | 255 |
18.计算3a3÷a2的结果是( )
| A. | 2a | B. | 3a2 | C. | 3a | D. | 3 |
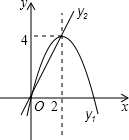 如图,已知抛物线y1=-x2+4x和直线y2=2x,我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.
如图,已知抛物线y1=-x2+4x和直线y2=2x,我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2. 的立方根是________,
的立方根是________, 的平方根是____________.
的平方根是____________.