题目内容
y=kx+4与两个坐标轴围成的三角形的面积为2,则k的值为
- A.4
- B.-4
- C.±2
- D.±4
D
分析:首先求出函数y=kx+4与两个坐标轴的交点,然后根据三角形的面积公式列出方程,即可求出k的值.
解答:由题意可知,当x=0时,y=4,即直线y=kx+4与y轴的交点为(0,4),
当y=0时,x=-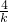 ,即与x轴的交点为(-
,即与x轴的交点为(-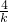 ,0),
,0),
故直线与两个坐标轴围成的三角形的面积为 ×4×|-
×4×|-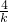 |=2,
|=2,
解得k=±4.
故选D.
点评:此题考查的是一次函数图象上点的坐标特点,即一次函数y=kx+b与x轴的交点为(- ,0),与y轴的交点为(0,b).
,0),与y轴的交点为(0,b).
分析:首先求出函数y=kx+4与两个坐标轴的交点,然后根据三角形的面积公式列出方程,即可求出k的值.
解答:由题意可知,当x=0时,y=4,即直线y=kx+4与y轴的交点为(0,4),
当y=0时,x=-
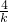 ,即与x轴的交点为(-
,即与x轴的交点为(-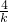 ,0),
,0),故直线与两个坐标轴围成的三角形的面积为
 ×4×|-
×4×|-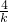 |=2,
|=2,解得k=±4.
故选D.
点评:此题考查的是一次函数图象上点的坐标特点,即一次函数y=kx+b与x轴的交点为(-
 ,0),与y轴的交点为(0,b).
,0),与y轴的交点为(0,b). 
练习册系列答案
相关题目
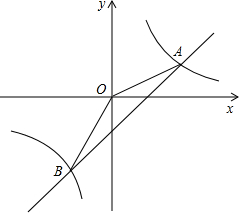 图象的两个交点,且第一象限内的点A的横坐标是它纵坐标的2倍,OA=
图象的两个交点,且第一象限内的点A的横坐标是它纵坐标的2倍,OA= b沿y轴向下平移3个单位后恰好经过原点,且抛物线的对称轴是直线x=-2.
b沿y轴向下平移3个单位后恰好经过原点,且抛物线的对称轴是直线x=-2. 的
的 图象的两个交点,且第一象限内的点A的横坐标是它纵坐标的2倍,OA=
图象的两个交点,且第一象限内的点A的横坐标是它纵坐标的2倍,OA=
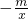 =0的解(直接写出答案);
=0的解(直接写出答案);