题目内容
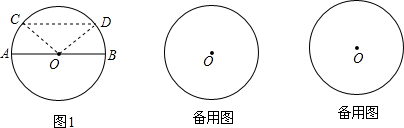
小惠在证明“两条平行弦所夹的弧相等”时，画了图1并连结半径OC，OD（即：AB为⊙O的直径，CD为弦且CD∥AB，求证：
=
）
（1）请按图1帮小惠证明当一条弦为直径时结论成立；
（2）显然，小惠只证了一条弦为直径的情形，失去了一般性．请你在下面两个备用图中画出其它情形，并尝试运用转化的思想，直接利用小惠的结论解决这个问题．
 |
| AC |
|
| BD |
（1）请按图1帮小惠证明当一条弦为直径时结论成立；
（2）显然，小惠只证了一条弦为直径的情形，失去了一般性．请你在下面两个备用图中画出其它情形，并尝试运用转化的思想，直接利用小惠的结论解决这个问题．
分析：（1）欲证明
=
，只需证明
与
所对的圆心角相等即可；
（2）分类讨论：①如备用图1，当平行弦在圆心两侧．作直径EF，使EF∥AB．利用（1）中的结论容易证得
=
，
=
，则
+
=
+
，即
=
；
②如备用图2，当平行弦在圆心一侧．作直径EF，使EF∥AB．利用（1）中的结论容易证得
=
，
=
，则
-
=
-
，即
=
．
|
| AC |
|
| BD |
|
| AC |
|
| BD |
（2）分类讨论：①如备用图1，当平行弦在圆心两侧．作直径EF，使EF∥AB．利用（1）中的结论容易证得
|
| AE |
|
| BF |
|
| CE |
|
| DF |
|
| AE |
|
| CE |
|
| BF |
|
| DF |
|
| AC |
|
| BD |
②如备用图2，当平行弦在圆心一侧．作直径EF，使EF∥AB．利用（1）中的结论容易证得
|
| AE |
|
| BF |
|
| CE |
|
| DF |
|
| AE |
|
| CE |
|
| BF |
|
| DF |
|
| AC |
|
| BD |
解答：
（1）证明：如图1，∵OC=OD，
∴∠1=∠2．
∵CD∥AB，
∴∠1=∠3，∠2=∠4，
∴∠3=∠4，
∴
=
；
（2）解：①如备用图1，当平行弦在圆心两侧．
作直径EF，使EF∥AB．
由（1）的结论可知，
=
．
∵CD∥AB，
∴EF∥CD，
∴
=
，
∴
+
=
+
，即
=
；
②如备用图2，当平行弦在圆心的两侧．
作直径EF，使EF∥AB．
∵CD∥AB，
∴EF∥CD，
由（1）的结论可知，
=
，
=
，
∴
-
=
-
，即
=
．
（1）证明：如图1，∵OC=OD，∴∠1=∠2．
∵CD∥AB，
∴∠1=∠3，∠2=∠4，
∴∠3=∠4，
∴
|
| AC |
|
| BD |
（2）解：①如备用图1，当平行弦在圆心两侧．
作直径EF，使EF∥AB．
由（1）的结论可知，
|
| AE |
|
| BF |
∵CD∥AB，
∴EF∥CD，
∴
|
| CE |
|
| DF |
∴
|
| AE |
|
| CE |
|
| BF |
|
| DF |
|
| AC |
|
| BD |
②如备用图2，当平行弦在圆心的两侧．
作直径EF，使EF∥AB．
∵CD∥AB，
∴EF∥CD，
由（1）的结论可知，
|
| AE |
|
| BF |
|
| CE |
|
| DF |
∴
|
| AE |
|
| CE |
|
| BF |
|
| DF |
|
| AC |
|
| BD |
点评：本题考查了圆的综合题．其中涉及到的知识点有圆心角、弧、弦的关系，平行线的性质．解答（2）题时，要分类讨论，并结合图形来解题，以降低题的难度与梯度．
练习册系列答案
相关题目