题目内容
(2000•安徽)如图,已知五边形ABCDE中,AC∥ED,交BE于点P,AD∥BC,交BE于点Q,BE∥CD、求证:△BCP≌△QDE.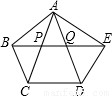
【答案】分析:先利用已知条件里的两组平行线AC∥ED,BE∥CD,可得到一个平行四边形,那么可得一组对应边相等,再利用AC∥ED,BC∥AD,可得两组对应角相等,利用AAS可证两个三角形全等.
解答:证明:∵AC∥ED,BE∥CD,
∴四边形PCDE是平行四边形.
∴PC=ED,
∵AC∥ED,BC∥AD,
∴∠BPC=∠QED,∠CBP=∠DQE,
在△BCP和△QDE中,
∵∠CBP=∠DQE,∠BPC=∠QED,PC=ED
∴△BCP≌△QDE.
点评:本题利用了平行四边形的判定和性质、平行线的性质、全等三角形的判定.
解答:证明:∵AC∥ED,BE∥CD,
∴四边形PCDE是平行四边形.
∴PC=ED,
∵AC∥ED,BC∥AD,
∴∠BPC=∠QED,∠CBP=∠DQE,
在△BCP和△QDE中,
∵∠CBP=∠DQE,∠BPC=∠QED,PC=ED
∴△BCP≌△QDE.
点评:本题利用了平行四边形的判定和性质、平行线的性质、全等三角形的判定.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
 absinC.
absinC.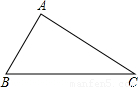
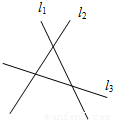
 absinC.
absinC.
