题目内容
 如图,已知一次函数y=-
如图,已知一次函数y=-| 3 |
| 4 |
(1)求线段AB的长;
(2)当t为何值时,△ACD的面积等于△AOB面积的
| 9 |
| 80 |
(3)当t为何值时,△ACD是等腰三角形.
分析:(1)首先容易求出A,B两点的坐标,然后求出OA,OB的长度,再利用勾股定理求AB;
(2)首先表示出△ACD的面积,求出△AOB的面积,再利用△ACD的面积等于△AOB面积的
求出即可;
(3)分别根据①当AC=AD时,②当AC=CD时,③当AD=CD时,利用相似三角形的性质求出即可.
(2)首先表示出△ACD的面积,求出△AOB的面积,再利用△ACD的面积等于△AOB面积的
| 9 |
| 80 |
(3)分别根据①当AC=AD时,②当AC=CD时,③当AD=CD时,利用相似三角形的性质求出即可.
解答: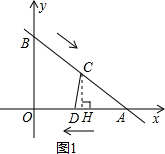 解:(1)当x=0时,y=3;当y=0时,x=4,
解:(1)当x=0时,y=3;当y=0时,x=4,
∴A(4,0),B(0,3),
∴OA=4,OB=3,
∴AB=
=5;
(2)如图1,作CH⊥OA于H,
则△ACH~△ABO,
∴
=
∴
=
∴CH=
∴S△ACD=
AD•CH=
t•
=-
t2+
t,
S△AOB=
OA•OB=
×4×3=6,
∴-
t2+
t=6×
,
即4t2-20t+9=0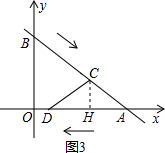
解得:t1=
,t2=
(舍去),
故t=
时,S△ACD=
S△AOB;
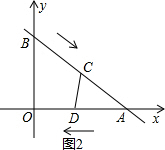
(3)①如图2,当AC=AD时,5-t=t,
∴解得:t=
(符合题意);
②如图3,当AC=CD时,过点C作CH⊥AD于点H,
由(2)得出:CH=
,AH=DH=
t,
∴
=
=
,
解得:t=
(符合题意),
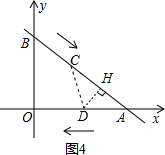
③如图4,当AD=CD时,过点D作DH⊥AB于点H,
∵∠OAB=∠HAD,∠DHA=∠BOA=90°,
∴△ADH∽ABO,
∴
=
,
=
解得:t=
(符合题意),
故t为
或
或
时△ACD是一个等腰三角形.
 解:(1)当x=0时,y=3;当y=0时,x=4,
解:(1)当x=0时,y=3;当y=0时,x=4,∴A(4,0),B(0,3),
∴OA=4,OB=3,
∴AB=
| 42+32 |
(2)如图1,作CH⊥OA于H,
则△ACH~△ABO,
∴
| CH |
| BO |
| AC |
| AB |

∴
| CH |
| 3 |
| 5-t |
| 5 |
∴CH=
| 3(5-t) |
| 5 |
∴S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3(5-t) |
| 5 |
=-
| 3 |
| 10 |
| 3 |
| 2 |
S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
∴-
| 3 |
| 10 |
| 3 |
| 2 |
| 9 |
| 80 |
即4t2-20t+9=0

解得:t1=
| 1 |
| 2 |
| 9 |
| 2 |
故t=
| 1 |
| 2 |
| 9 |
| 80 |
(3)①如图2,当AC=AD时,5-t=t,
∴解得:t=
| 5 |
| 2 |
②如图3,当AC=CD时,过点C作CH⊥AD于点H,
由(2)得出:CH=
| 3(5-t) |
| 5 |
| 1 |
| 2 |
∴
| CH |
| AH |
| ||
|
| 3 |
| 4 |

解得:t=
| 40 |
| 13 |
③如图4,当AD=CD时,过点D作DH⊥AB于点H,
∵∠OAB=∠HAD,∠DHA=∠BOA=90°,
∴△ADH∽ABO,
∴
| AH |
| AO |
| AD |
| AB |
| ||
| 4 |
| t |
| 5 |
解得:t=
| 25 |
| 13 |
故t为
| 5 |
| 2 |
| 40 |
| 13 |
| 25 |
| 13 |
点评:此题主要考查了等腰三角形的判定与性质以及相似三角形的判定与性质和勾股定理等知识,利用分类讨论得出是解题关键,不要漏解.

练习册系列答案
相关题目
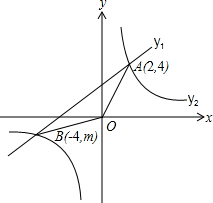 B(-4,m)两点.
B(-4,m)两点. 如图,已知一次函数y=kx+b的图象与反比例函数y=-
如图,已知一次函数y=kx+b的图象与反比例函数y=- (2013•新疆)如图,已知一次函数y1=kx+b与反比例函数
(2013•新疆)如图,已知一次函数y1=kx+b与反比例函数 如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位后刚好在反比例函数
如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位后刚好在反比例函数 如图,已知一次函数y=kx+b的图象交反比例函数
如图,已知一次函数y=kx+b的图象交反比例函数