��Ŀ����
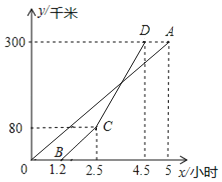
����Ŀ����ͼ��������C1��![]() �Ķ���ΪA����x��������ύ�ڵ�B.
�Ķ���ΪA����x��������ύ�ڵ�B.
��1����ֱ��д��A��B��������꣬A ��B .
��2����������C1�ϵĵ�ĺ�����������궼����ԭ����2������任��õ��������ߵĽ���ʽ��
��3����������C1�ϵĵ㣨x��y����Ϊ��kx��ky����|k|��1�����任��õ�����������C2.������C2�Ķ���ΪC����P��������C2�ϣ�����S��PAC��S��ABC���ҡ�ACP��90��.
�ٵ�k��1ʱ����k��ֵ��
�ڵ�k��-1ʱ������ֱ��д��k��ֵ������˵������.
���𰸡�(1)A(1,![]() );B(2,0);(2) y=-
);B(2,0);(2) y=-![]() x2+2
x2+2![]() x����3����
x����3����![]() ���� -
���� -![]() .
.
��������
��1���Ѻ�������ʽ��Ϊ����ʽ���ɵõ�A��1��![]() �����ⷽ�̼��ɵõ�B��2��0����
�����ⷽ�̼��ɵõ�B��2��0����
��2����������C1����ʽ���A��B��ԭ�����꣬���������궼����ԭ����2��������ϵ�����ɵã�
��3������ͼ1�У���k��1ʱ���루1��ͬ���ɵ�������C2�Ľ���ʽΪy=-![]() x2+2
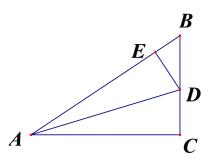
x2+2![]() x������C�����꣬����S��PAC=S��ABC֪BP��AC���̶��ɵ���ABO�DZ߳�Ϊ2���������Σ��ı���CEBP�Ǿ��Σ���ʾ����P�����꣬������뵽������C2����ʽ�����k��ֵ��
x������C�����꣬����S��PAC=S��ABC֪BP��AC���̶��ɵ���ABO�DZ߳�Ϊ2���������Σ��ı���CEBP�Ǿ��Σ���ʾ����P�����꣬������뵽������C2����ʽ�����k��ֵ��
����ͼ2�У���k��-1ʱ������ABO����y��ԳƵ���A��B��O��OE����A��B����ͬ���ɵ��ı���CEBP�Ǿ��Σ������������C2����ʽ����ʾ����P�����꣬������뵽������C2����ʽ�����k��ֵ��
(1)A(1,![]() );B(2,0);
);B(2,0);
��2����y=-![]() x2+2
x2+2![]() x=-
x=-![]() ��x-1��2+
��x-1��2+![]() ��
��
��������C1����ԭ��O����A��1��![]() ���͵�B��2��0�����㣬
���͵�B��2��0�����㣬
��任��������߾���ԭ��O����2��2![]() ���ͣ�4��0�����㣬
���ͣ�4��0�����㣬
��任�������ߵĽ���ʽΪy=-![]() x2+2
x2+2![]() x��
x��
��3������ͼ1�У���k��1ʱ��

��������C2����ԭ��O����k��![]() k������2k��0�����㣬
k������2k��0�����㣬
��������C2�Ľ���ʽΪy=-![]() x2+2
x2+2![]() x��
x��
��O��A��C���㹲�ߣ��Ҷ���CΪ��k��![]() k����
k����
��ͼ����S��PAC=S��ABC����BP��AC��
����P��PD��x����D������B��BE��AO��E��
������֪��ABO�DZ߳�Ϊ2���������Σ��ı���CEBP�Ǿ��Σ�
��OE=1��CE=BP=2k-1��
�ߡ�PBD=60�㣬��BD=k-![]() ��PD=
��PD=![]() ��2k-1����
��2k-1����
��P��k+![]() ��
��![]() ��2k-1������
��2k-1������
��![]() ��2k-1��=-
��2k-1��=-![]() ��k+
��k+![]() ��2+2
��2+2![]() ��k+
��k+![]() ����
����
��ã�k=![]() ��
��
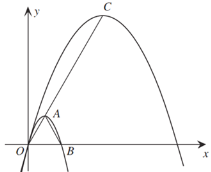
����ͼ2�У���k��-1ʱ��

��������C2����ԭ��O����k��![]() k������2k��0�����㣬
k������2k��0�����㣬
��������C2�Ľ���ʽΪy=-![]() x2+2
x2+2![]() x��
x��
��O��A��C�����㹲�ߣ��Ҷ���C��Ϊ��k��![]() k����
k����
����ABO����y��ԳƵ���A��B��O��OE����A��B�䣬
��S��PAC��=S��ABC=S��AC��B����
��A��P��AC�����������ı���PC��OE���Ǿ��Σ�
��PE��=OC��=-2k��B��E��=1��PB��=-2k-1��
��Rt��PDB���У��ߡ�PDB��=90�㣬��PB��D=��A��B��O=60�㣬
��DB��=![]() PB��=
PB��=![]() ��DP=
��DP=![]() ��-2k-1�������P����[
��-2k-1�������P����[![]() ��
��![]() ��2k+1��]��
��2k+1��]��
��![]() ��2k+1��=-
��2k+1��=-![]() ��
��![]() ��2+2
��2+2![]() ��
��![]() ��
��
��k=-![]() ��
��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�