Question

【题目】如图，在菱形中，对角线、相交于点．，，点为上一动点，点以的速度从点出发沿向点运动．设运动时间为，当________时，为等腰三角形．

Answer 1

【答案】或或

【解析】

求出BA的值，根据已知画出符合条件的三种情况：①当PA=AB=5cm时，②当P和C重合时，PB=AB=5cm，③作AB的垂直平分线交AC于P，此时PB=PA，连接PB，求出即可．

∵四边形ABCD是菱形，AC=8cm，BD=6cm，

∴AC⊥BD，AO=OC=4cm，BO=OD=3cm，

由勾股定理得：BC=AB=AD=CD=5cm，

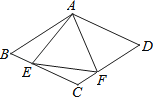
分为三种情况：①如图1，当PA=AB=5cm时，t=5÷1=5（s）；

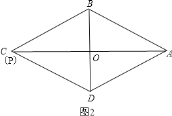
②如图2，当P和C重合时，PB=AB=5cm，t=8÷1=8（s）；

③如图3，作AB的垂直平分线交AC于P，此时PB=PA，连接PB，

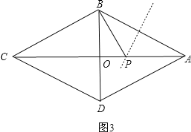
在Rt△BOP中，由勾股定理得：BP2=BO2+OP2，

AP2=32+（4-AP）2，

AP=，

t=÷1=（s），

故答案为：5或8或.