题目内容
(2012•株洲)如图,在△ABC中,∠C=90°,BC=5米,AC=12米.M点在线段CA上,从C向A运动,速度为1米/秒;同时N点在线段AB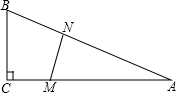 上,从A向B运动,速度为2米/秒.运动时间为t秒.
上,从A向B运动,速度为2米/秒.运动时间为t秒.
(1)当t为何值时,∠AMN=∠ANM?
(2)当t为何值时,△AMN的面积最大?并求出这个最大值.
 上,从A向B运动,速度为2米/秒.运动时间为t秒.
上,从A向B运动,速度为2米/秒.运动时间为t秒.(1)当t为何值时,∠AMN=∠ANM?
(2)当t为何值时,△AMN的面积最大?并求出这个最大值.
分析:(1)用t表示出AM和AN的值,根据AM=AN,得到关于t的方程求得t值即可;
(2)作NH⊥AC于H,证得△ANH∽△ABC,从而得到比例式,然后用t表示出NH,从而计算其面积得到有关t的二次函数求最值即可.
(2)作NH⊥AC于H,证得△ANH∽△ABC,从而得到比例式,然后用t表示出NH,从而计算其面积得到有关t的二次函数求最值即可.
解答:解:(1)∵从C向A运动,速度为1米/秒;同时N点在线段AB上,从A向B运动,速度为2米/秒.运动时间为t秒.
∴AM=12-t,AN=2t
∵∠AMN=∠ANM
∴AM=AN,从而12-t=2t
解得:t=4 秒,
∴当t为4时,∠AMN=∠ANM.
(2)在Rt△ABC中
∵AB2=BC2+AC2
∴AB=13
如图,作NH⊥AC于H,
∴∠NHA=∠C=90°,
∵∠A是公共角,
∴△NHA∽△BCA
∴
=
,
即:
=
,
∴NH=
t
从而有S△AMN=
(12-t)•
t=-
t2+
t,
∴当t=6时,S最大值=
.
∴AM=12-t,AN=2t
∵∠AMN=∠ANM
∴AM=AN,从而12-t=2t
解得:t=4 秒,
∴当t为4时,∠AMN=∠ANM.

(2)在Rt△ABC中
∵AB2=BC2+AC2
∴AB=13
如图,作NH⊥AC于H,
∴∠NHA=∠C=90°,
∵∠A是公共角,
∴△NHA∽△BCA
∴
| AN |
| AB |
| NH |
| BC |
即:
| 2t |
| 13 |
| NH |
| 5 |
∴NH=
| 10 |
| 13 |
从而有S△AMN=
| 1 |
| 2 |
| 10 |
| 13 |
| 5 |
| 13 |
| 60 |
| 13 |
∴当t=6时,S最大值=
| 180 |
| 13 |
点评:本题考查了相似三角形的判定与性质,解题的关键是根据证得的相似三角形得到比例式,从而求解.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
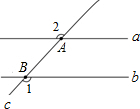 (2012•株洲)如图,已知直线a∥b,直线c与a、b分别交于A、B;且∠1=120°,则∠2=( )
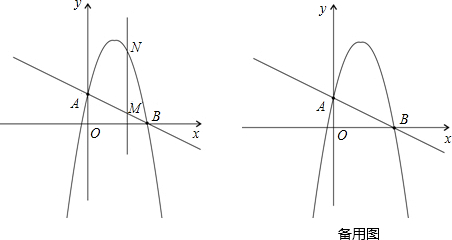
(2012•株洲)如图,已知直线a∥b,直线c与a、b分别交于A、B;且∠1=120°,则∠2=( ) (2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )
(2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )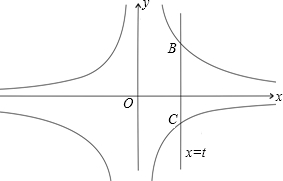 (2012•株洲)如图,直线x=t(t>0)与反比例函数
(2012•株洲)如图,直线x=t(t>0)与反比例函数 (2012•株洲)如图,已知AD为⊙O的直径,B为AD延长线上一点,BC与⊙O切于C点,∠A=30°.
(2012•株洲)如图,已知AD为⊙O的直径,B为AD延长线上一点,BC与⊙O切于C点,∠A=30°.