题目内容
已知如图所示,折叠长方形的一边AD,使点D落在边BC的点F处,已知AB=8cm,BC=10cm,求EC的长.

解:根据题意得:Rt△ADE Rt△AFE,
Rt△AFE,
∴∠AFE=90°,AF=AD=BC=10cm,EF=ED,
设EC=xcm,则ED=EF=CD﹣EC=8﹣x,
在Rt△ABF中,
由勾股定理得:AB2+BF2=AF2,即82+BF2=102,
∴BF=6cm,
∴CF=BC﹣BF=10﹣6=4cm,
在Rt△ECF中,
由勾股定理可得:EF2=EC2+CF2,即(8﹣x)2=x2+42,
∴64﹣16x+x2=x2+16,
解得:x=3cm,即CE=3cm.
 Rt△AFE,
Rt△AFE,∴∠AFE=90°,AF=AD=BC=10cm,EF=ED,
设EC=xcm,则ED=EF=CD﹣EC=8﹣x,
在Rt△ABF中,
由勾股定理得:AB2+BF2=AF2,即82+BF2=102,
∴BF=6cm,
∴CF=BC﹣BF=10﹣6=4cm,
在Rt△ECF中,
由勾股定理可得:EF2=EC2+CF2,即(8﹣x)2=x2+42,
∴64﹣16x+x2=x2+16,
解得:x=3cm,即CE=3cm.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
 如图所示,折叠矩形ABCD的一边AD,使点D落在BC边上的点F处,已知AB=8cm,BC=10cm,
如图所示,折叠矩形ABCD的一边AD,使点D落在BC边上的点F处,已知AB=8cm,BC=10cm,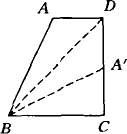
 ,使点
,使点 落在边
落在边 的点
的点 处,已知
处,已知
 ,求
,求 的长。
的长。
 ,使点
,使点 落在边
落在边 的点
的点 处,已知
处,已知
 ,求
,求 的长。
的长。