题目内容
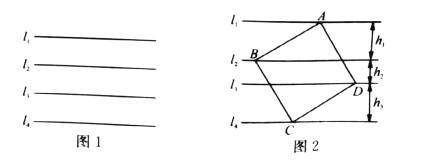
【题目】直线![]() 是同一平面内的一组平行线.
是同一平面内的一组平行线.
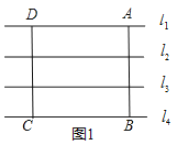
(1)如图1.正方形![]() 的4个顶点都在这些平行线上,若四条直线中相邻两条之间的距离都是1,其中点
的4个顶点都在这些平行线上,若四条直线中相邻两条之间的距离都是1,其中点![]() ,点
,点![]() 分别在直线
分别在直线![]() 和
和![]() 上,求正方形的面积;
上,求正方形的面积;
(2)如图2,正方形![]() 的4个顶点分别在四条平行线上,若四条直线中相邻两条之间的距离依次为
的4个顶点分别在四条平行线上,若四条直线中相邻两条之间的距离依次为![]() .
.
①求证:![]() ;
;
②设正方形![]() 的面积为
的面积为![]() ,求证
,求证![]() .
.
【答案】(1)9或5;(2)①见解析,②见解析
【解析】
(1)分两种情况:①如图1-1,得出正方形ABCD的边长为3,求出正方形ABCD的面积为9;
②如图1-2,过点B作EF⊥l1于E,交l4于F,则EF⊥l4,证明△ABE≌△BCF(AAS),得出AE=BF=2由勾股定理求出AB=![]() ,即可得出答案;
,即可得出答案;
(2)①过点B作EF⊥l1于E,交l4于F,作DM⊥l4于M,证明△ABE≌△BCF(AAS),得出AE=BF,同理△CDM≌△BCF(AAS),得出△ABE≌△CDM(AAS),得出BE=DM即可;
②由①得出AE=BF=h2+h3=h2+h1,得出正方形ABCD的面积S=AB2=AE2+BE2,即可得到答案.
解:(1)①如图,当点![]() 分别在
分别在![]() 上时,面积为:
上时,面积为:![]() ;
;
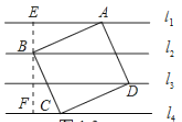
②如图,当点![]() 分别在
分别在![]() 上时,过点B作EF⊥l1于E,交l4于F,则EF⊥l4,
上时,过点B作EF⊥l1于E,交l4于F,则EF⊥l4,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠ABE+∠CBF=180°-90°=90°,
∵∠CBF+∠BCF=90°,
∴∠ABE=∠BCF,
在△ABE和△BCF中
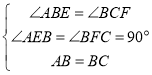 ,
,
∴△ABE≌△BCF(AAS),
∴AE=BF=2,
∴AB=![]() ,
,
∴正方形ABCD的面积=AB2=5;
综上所述,正方形ABCD的面积为9或5;
(2)①证明:过点B作EF⊥l1于E,交l4于F,作DM⊥l4于M,如图所示:则EF⊥l4,
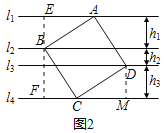
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠ABE+∠CBF=180°-90°=90°,
∵∠CBF+∠BCF=90°,
∴∠ABE=∠BCF,
在△ABE和△BCF中,
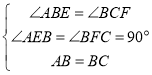 ,
,
∴△ABE≌△BCF(AAS),
∴AE=BF,
同理△CDM≌△BCF(AAS),
∴△ABE≌△CDM(AAS),
∴BE=DM,
即h1=h3.
②解:由①得:AE=BF=h2+h3=h2+h1,
∵正方形ABCD的面积:S=AB2=AE2+BE2,
∴S=(h2+h1)2+h12=2h12+2h1h2+h22.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案