题目内容
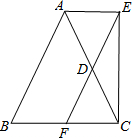 已知,如图在△ABC中,AB=AC,点D是AC的中点,直线AE∥BC,过D点作直线EF∥AB分别交AE、BC于点E、F,求证:四边形AECF是矩形.
已知,如图在△ABC中,AB=AC,点D是AC的中点,直线AE∥BC,过D点作直线EF∥AB分别交AE、BC于点E、F,求证:四边形AECF是矩形.分析:根据中点定义求出DA=DC,根据两直线平行,内错角相等可得∠AED=∠CFD,然后利用“角角边”证明△ADE和△CDF全等,根据全等三角形对应边相等可得AE=CF,然后根据一组对边平行且相等的四边形是平行四边形判断出四边形AECF是平行四边形,再判断出四边形ABFE是平行四边形,根据平行四边形对边相等可得AB=EF,然后求出AC=EF,然后根据对角线相等的平行四边形是矩形证明即可.
解答: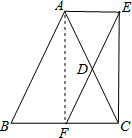 证明:∵点D是AC的中点,
证明:∵点D是AC的中点,
∴DA=DC,
∵AE∥BC,
∴∠AED=∠CFD,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(AAS),
∴AE=CF,
又∵AE∥BC,
∴四边形AECF是平行四边形,
∵AE∥BC,EF∥AB,
∴四边形ABFE是平行四边形,
∴AB=EF,
∵AB=AC,
∴AC=EF,
∴四边形AECF是矩形.
 证明:∵点D是AC的中点,
证明:∵点D是AC的中点,∴DA=DC,
∵AE∥BC,
∴∠AED=∠CFD,
在△ADE和△CDF中,
|
∴△ADE≌△CDF(AAS),
∴AE=CF,
又∵AE∥BC,
∴四边形AECF是平行四边形,
∵AE∥BC,EF∥AB,
∴四边形ABFE是平行四边形,
∴AB=EF,
∵AB=AC,
∴AC=EF,
∴四边形AECF是矩形.
点评:本题考查了矩形的判定,主要利用了全等三角形的判定与性质,平行四边形的判定与性质,对角线相等的平行四边形是矩形的判定方法.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
 已知:如图在△ABC中,DE∥BC,
已知:如图在△ABC中,DE∥BC,| AD |
| DB |
| 1 |
| 3 |
| DE |
| BC |
A、
| ||
B、
| ||
C、
| ||
D、
|
 9、已知:如图在△ABC中,AD平分∠BAC,AD⊥BC,则△ACD≌△ABD的根据是
9、已知:如图在△ABC中,AD平分∠BAC,AD⊥BC,则△ACD≌△ABD的根据是 已知,如图在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG平分∠CDE,DC=AE,
已知,如图在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG平分∠CDE,DC=AE, 已知:如图在△ABC中,∠C=90°,BD是∠ABC的内角平分线,
已知:如图在△ABC中,∠C=90°,BD是∠ABC的内角平分线, 已知,如图在△ABC中,∠ACB=90°,AC=8,BC=6,CD、CE分别是斜边AB上的中线和高.则下列结论错误的是( )
已知,如图在△ABC中,∠ACB=90°,AC=8,BC=6,CD、CE分别是斜边AB上的中线和高.则下列结论错误的是( )