题目内容
若正△ABC的边长为a，则它的外接圆的面积为
．
| a2π |
| 3 |
| a2π |
| 3 |
分析：先根据题意画出图形，求出正△ABC外接圆的半径，利用圆的面积公式即可得出结论．
解答：
解：如图所示：
∵△ABC是等边三角形，BC=a，
∴∠OBD=30°，BD=
，
∴OB=
=
=
=
，
∴外接圆的面积=πOB2=（
）2π=
．
故答案为：
．
解：如图所示：∵△ABC是等边三角形，BC=a，
∴∠OBD=30°，BD=
| a |
| 2 |
∴OB=
| BD |
| cos∠OBD |
| ||
| cos30° |
| ||||
|
| ||
| 3 |
∴外接圆的面积=πOB2=（
| ||
| 3 |
| a2π |
| 3 |
故答案为：
| a2π |
| 3 |
点评：本题考查的是三角形的外接圆与外心，根据题意画出图形，利用锐角三角函数的定义求出△ABC的外接圆的半径是解答此题的关键．
练习册系列答案
相关题目
如图，△ABC为正三角形，D，E分别为AC，BC上的点（不在顶点），∠BDE=60°．（1）求证：△DEC∽△BDA；
（2）若正△ABC的边长为6，并设DC=x，BE=y．试求y与x之间的函数关系式．
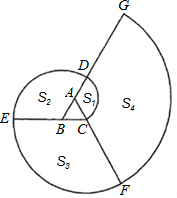依次为A、B、C…．当渐开线延伸开时，形成三个扇形S1、S2、S3和一系列扇环S4、S5、…若正△ABC的边长为1．
如图，△ABC为正三角形，D，E分别为AC，BC上的点（不在顶点），∠BDE=60°．