题目内容
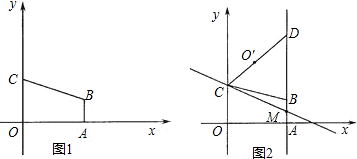
如图1，直线L：y=-x+3与x轴、y轴分别交于点B、点C，经过B、C两点的抛物线G：y=ax2+bx+c与x轴的另一交点为A，顶点为P，且对称轴是直线x=2．
（1）该抛物线G的解析式为
（2）将直线L沿y轴向下平移
个单位长度，能使它与抛物线G只有一个公共点；
（3）若点E在抛物线G的对称轴上，点F在该抛物线上，且以点A、B、E、F为顶点的四边形为平行四边形，求点E与点F坐标并直接写出平行四边形的周长．
（4）连接AC，得△ABC．若点Q在x轴上，且以点P、B、Q为顶点的三角形与△ABC相似，求点Q的坐标．
（1）该抛物线G的解析式为
y=x2-4x+3
y=x2-4x+3
；（2）将直线L沿y轴向下平移
| 9 |
| 4 |
| 9 |
| 4 |
（3）若点E在抛物线G的对称轴上，点F在该抛物线上，且以点A、B、E、F为顶点的四边形为平行四边形，求点E与点F坐标并直接写出平行四边形的周长．
（4）连接AC，得△ABC．若点Q在x轴上，且以点P、B、Q为顶点的三角形与△ABC相似，求点Q的坐标．
分析：（1）先根据直线的解析式求出点B、C的坐标，再根据二次函数的对称性求出点A的坐标，然后利用待定系数法列式求解即可得到抛物线G的解析式；
（2）根据平移的性质，设平移后的直线的解析式为y=-x+b，与抛物线的解析式联立得到关于x的一元二次方程，再根据△=0时，有一个交点列式求出b的值，再根据平移的性质解答；
（3）因为AB是边长还是对角线不明确，所以分①AB是边长时，根据平行四边形的对边平行且相等得到EF=AB=2，从而得到点F的横坐标，代入抛物线解析式求出纵坐标的值，从而得到点E、F的坐标；②AB是对角线时，根据平行四边形的对角线互相平分，再结合二次函数的性质可得EF⊥AB时，满足条件，从而求出点E、F的坐标；
（4）根据点A、B、C、P的坐标可知，∠PBQ=∠ABC=45°，并求出AB、BC、PB的长度，然后分①PB与AB是对应边，②PB与BC是对应边时两种情况，利用相似三角形对应边成比例列式求出BQ的长度，从而点Q的坐标可得，③点Q在点B的右侧时，∠PBx=180°-45°=135°，∠BAC＜135，不存在以点P、B、Q为顶点的三角形与△ABC相似．
（2）根据平移的性质，设平移后的直线的解析式为y=-x+b，与抛物线的解析式联立得到关于x的一元二次方程，再根据△=0时，有一个交点列式求出b的值，再根据平移的性质解答；
（3）因为AB是边长还是对角线不明确，所以分①AB是边长时，根据平行四边形的对边平行且相等得到EF=AB=2，从而得到点F的横坐标，代入抛物线解析式求出纵坐标的值，从而得到点E、F的坐标；②AB是对角线时，根据平行四边形的对角线互相平分，再结合二次函数的性质可得EF⊥AB时，满足条件，从而求出点E、F的坐标；
（4）根据点A、B、C、P的坐标可知，∠PBQ=∠ABC=45°，并求出AB、BC、PB的长度，然后分①PB与AB是对应边，②PB与BC是对应边时两种情况，利用相似三角形对应边成比例列式求出BQ的长度，从而点Q的坐标可得，③点Q在点B的右侧时，∠PBx=180°-45°=135°，∠BAC＜135，不存在以点P、B、Q为顶点的三角形与△ABC相似．
解答：解：（1）当x=0时，y=3，
当y=0时，-x+3=0，解得x=3，
∴点B、C的坐标为B（3，0），C（0，3），
又∵抛物线过x轴上的A，B两点，且对称轴为x=2，
根据抛物线的对称性，
∴点A的坐标为（1，0），
∴
，
解得
，
∴抛物线的解析式为y=x2-4x+3；
（2）设平移后的直线解析式为y=-x+b，
则
，
∴x2-3x+3-b=0，
∵它与抛物线G只有一个公共点，
∴△=b2-4ac=（-3）2-4×1×（3-b）=9-12+4b=0，
解得b=
，
3-
=
，
∴向下平移了
个单位；
（3）∵A（1，0），B（3，0），
∴AB=3-1=2，
①当AB是边时，∵点E在对称轴上，平行四边形的对边平行且相等，
∴EF=AB=2，
∴点F的横坐标为0或4，
当横坐标为0时，y=02-4×0+3=3，
当横坐标为4时，y=42-4×4+3=3，
∴点F的坐标为F1（0，3）或F2（4，3），
此时点E的坐标为E1（2，3），
此时AE=
=
，
∴平行四边形的周长为：2（AB+AE）=2（2+
）=4+2
；
②当AB边为对角线时，EF与AB互相垂直平分，
∵y=x2-4x+3=（x-2）2-1，
∴此时点E、F的坐标为E2（2，1），F3（2，-1），
∴AE=
=
，
AF=
=
，
∴平行四边形的周长为：2（AE+AF）=2（
+
）=4
，
综上所述，点E、F的坐标分别为E1（2，3），F1（0，3）或F2（4，3），此时平行四边形的周长为4+2
，
或E2（2，1），F3（2，-1），此时平行四边形的周长为4
；
（4）连接PB，由y=x2-4x+3=（x-2）2-1，得P（2，-1），
设抛物线的对称轴交x轴于点M，
∵在Rt△PBM中，PM=MB=1，
∴∠PBM=45°，PB=
．
由点B（3，0），C（0，3）易得OB=OC=3，在等腰直角三角形OBC中，∠ABC=45°，
由勾股定理，得BC=3
．
假设在x轴上存在点Q，使得以点P，B，Q为顶点的三角形与△ABC相似．
①PB与AB是对应边时，∵∠PBQ=∠ABC=45°，
∴
=
，
即
=
，
解得BQ=3，
又∵BO=3，
∴点Q与点O重合，
∴Q1的坐标是（0，0），
②PB与BC是对应边时，∵∠PBQ=∠ABC=45°，
∴
=
，
即
=
，
解得QB=
，
∵OB=3，
∴OQ=OB-QB=3-
=
，
∴Q2的坐标是（
，0），
③∵∠PBx=180°-45°=135°，∠BAC＜135°，
∴∠PBx≠∠BAC．
∴点Q不可能在B点右侧的x轴上
综上所述，在x轴上存在两点Q1（0，0），Q2（
，0），能使得以点P，B，Q为顶点的三角形与△ABC相似．
当y=0时，-x+3=0，解得x=3，
∴点B、C的坐标为B（3，0），C（0，3），
又∵抛物线过x轴上的A，B两点，且对称轴为x=2，
根据抛物线的对称性，
∴点A的坐标为（1，0），
∴
|
解得
|
∴抛物线的解析式为y=x2-4x+3；
（2）设平移后的直线解析式为y=-x+b，
则
|
∴x2-3x+3-b=0，
∵它与抛物线G只有一个公共点，
∴△=b2-4ac=（-3）2-4×1×（3-b）=9-12+4b=0，
解得b=
| 3 |
| 4 |
3-
| 3 |
| 4 |
| 9 |
| 4 |
∴向下平移了
| 9 |
| 4 |
（3）∵A（1，0），B（3，0），
∴AB=3-1=2，
①当AB是边时，∵点E在对称轴上，平行四边形的对边平行且相等，
∴EF=AB=2，
∴点F的横坐标为0或4，
当横坐标为0时，y=02-4×0+3=3，
当横坐标为4时，y=42-4×4+3=3，
∴点F的坐标为F1（0，3）或F2（4，3），
此时点E的坐标为E1（2，3），
此时AE=
| 12+32 |
| 10 |
∴平行四边形的周长为：2（AB+AE）=2（2+
| 10 |
| 10 |
②当AB边为对角线时，EF与AB互相垂直平分，
∵y=x2-4x+3=（x-2）2-1，
∴此时点E、F的坐标为E2（2，1），F3（2，-1），
∴AE=
| 12+12 |
| 2 |
AF=
| 12+12 |
| 2 |
∴平行四边形的周长为：2（AE+AF）=2（
| 2 |
| 2 |
| 2 |
综上所述，点E、F的坐标分别为E1（2，3），F1（0，3）或F2（4，3），此时平行四边形的周长为4+2
| 10 |
或E2（2，1），F3（2，-1），此时平行四边形的周长为4
| 2 |
（4）连接PB，由y=x2-4x+3=（x-2）2-1，得P（2，-1），
设抛物线的对称轴交x轴于点M，
∵在Rt△PBM中，PM=MB=1，
∴∠PBM=45°，PB=
| 2 |
由点B（3，0），C（0，3）易得OB=OC=3，在等腰直角三角形OBC中，∠ABC=45°，
由勾股定理，得BC=3
| 2 |
假设在x轴上存在点Q，使得以点P，B，Q为顶点的三角形与△ABC相似．
①PB与AB是对应边时，∵∠PBQ=∠ABC=45°，
∴
| BQ |
| BC |
| PB |
| AB |
即
| BQ | ||
3
|
| ||
| 2 |
解得BQ=3，
又∵BO=3，
∴点Q与点O重合，
∴Q1的坐标是（0，0），
②PB与BC是对应边时，∵∠PBQ=∠ABC=45°，
∴
| QB |
| AB |
| PB |
| BC |
即
| QB |
| 2 |
| ||
3
|
解得QB=
| 2 |
| 3 |
∵OB=3，
∴OQ=OB-QB=3-
| 2 |
| 3 |
| 7 |
| 3 |
∴Q2的坐标是（
| 7 |
| 3 |
③∵∠PBx=180°-45°=135°，∠BAC＜135°，
∴∠PBx≠∠BAC．
∴点Q不可能在B点右侧的x轴上
综上所述，在x轴上存在两点Q1（0，0），Q2（
| 7 |
| 3 |
点评：本题着重考查了待定系数法求二次函数解析式、平行四边形的判定和性质等知识点，综合性强，考查学生分类讨论，数形结合的数学思想方法，注意要分情况讨论求解．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
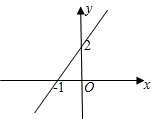如图，该直线是某个一次函数的图象，则此函数的解析式为
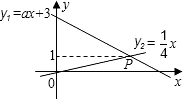如图，两直线y1=ax+3与y2=