题目内容
如图，是△ABC和⊙O的重叠情形，⊙O与直线BC相切于点C，且与AC交于另一点D．若∠A=70°，∠B=60°，则∠COD的度数为（ ）分析：首先利用三角形内角和定理即可求得∠ACB的度数，然后利用弦切角定理即可求解．
解答：解：∵△ABC中，∠ACB=180°-∠A-∠B=180°-70°-60°=50°，
又∵BC是圆的切线，
∴∠COD=2∠ACB=2×50°=100°．
故选C．
又∵BC是圆的切线，
∴∠COD=2∠ACB=2×50°=100°．
故选C．
点评：本题考查了三角形的内角和定理以及弦切角定理，正确理解定理是关键．
练习册系列答案
相关题目
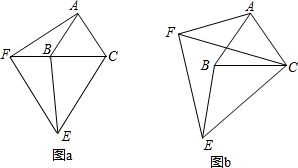
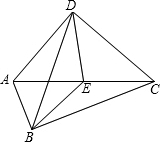已知：如图，Rt△ABC和Rt△ADC，∠ABC=∠ADC=90°，点E是AC的中点．
如图，是△ABC和⊙O的重叠情形，⊙O与直线BC相切于点C，且与AC交于另一点D．若∠A=70°，∠B=60°，则∠COD的度数为