题目内容
如图，沿OA将圆锥侧面剪开，展开成平面图形是扇形OAB．
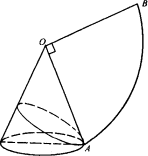
(1)扇形的弧AB的长与圆锥底面圆周的长是怎样的关系？点A和点B在圆锥的侧面上是怎样的位置关系？
(2)若∠AOB＝90°，占A在圆锥侧面上运动一圈后又回到原位，则点A运动的最短路程应怎样设计(设底面圆半径为r)？若r＝
且∠AOB＝90°，求点A运动的最短路程．
答案：
解析：
解析：
|
(1)长度相等，重合； (2)连接AB，线段AB的长即为所求，设扇形OAB的半径为R，可求得R＝4r，当r＝ |
时，AB＝
R＝4
练习册系列答案
名校课堂系列答案
相关题目
4、已知O为圆锥的顶点，M为圆锥底面上一点，点P在OM上．一只蜗牛从P点出发，绕圆锥侧面爬行，回到P点时所爬过的最短路线的痕迹如图所示．若沿OM将圆锥侧面剪开并展开，所得侧面展开图是（ ）
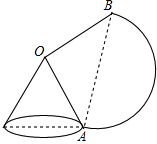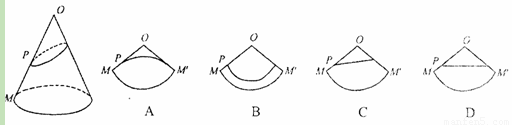
如图，沿OA将圆锥侧面剪开，展开成平面图形后是扇形OAB．
如图，沿OA将圆锥侧面剪开，展开成平面图形后是扇形OAB．