题目内容
观察下列各式及其验证过程:
验证: =
=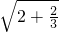 ;
;
验证: =
= =
= =
=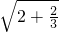 ;
;
验证: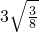 =
= ;
;
验证: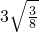 =
= =
= =
= .
.
(1)按照上述两个等式及其验证过程的基本思路,猜想4 的变形结果并进行验证;
的变形结果并进行验证;
(2)针对上述各式反映的规律,写出用n(n为任意自然数,且n≥2)表示的等式,并给出证明.
解:(1) .验证如下:
.验证如下:
左边= =
= =
= =
= =右边,
=右边,
故猜想正确;
(2) .证明如下:
.证明如下:
左边= =
= =
= =
= =右边.
=右边.
分析:(1)通过观察,不难发现:等式的变形过程利用了二次根式的性质a= (a≥0),把根号外的移到根号内;再根据“同分母的分式相加,分母不变,分子相加”这一法则的倒用来进行拆分,同时要注意因式分解进行约分,最后结果中的被开方数是两个数相加,两个加数分别是左边根号外的和根号内的;
(a≥0),把根号外的移到根号内;再根据“同分母的分式相加,分母不变,分子相加”这一法则的倒用来进行拆分,同时要注意因式分解进行约分,最后结果中的被开方数是两个数相加,两个加数分别是左边根号外的和根号内的;
(2)根据上述变形过程的规律,即可推广到一般.表示左边的式子时,注意根号外的和根号内的分子、分母之间的关系:根号外的和根号内的分子相同,根号内的分子是分母的平方减去1.
点评:此题是一个找规律的题目,主要考查了二次根式的性质.观察时,既要注意观察等式的左右两边的联系,还要注意右边必须是一种特殊形式.
 .验证如下:
.验证如下:左边=
 =
= =
= =
= =右边,
=右边,故猜想正确;
(2)
 .证明如下:
.证明如下:左边=
 =
= =
= =
= =右边.
=右边.分析:(1)通过观察,不难发现:等式的变形过程利用了二次根式的性质a=
 (a≥0),把根号外的移到根号内;再根据“同分母的分式相加,分母不变,分子相加”这一法则的倒用来进行拆分,同时要注意因式分解进行约分,最后结果中的被开方数是两个数相加,两个加数分别是左边根号外的和根号内的;
(a≥0),把根号外的移到根号内;再根据“同分母的分式相加,分母不变,分子相加”这一法则的倒用来进行拆分,同时要注意因式分解进行约分,最后结果中的被开方数是两个数相加,两个加数分别是左边根号外的和根号内的;(2)根据上述变形过程的规律,即可推广到一般.表示左边的式子时,注意根号外的和根号内的分子、分母之间的关系:根号外的和根号内的分子相同,根号内的分子是分母的平方减去1.
点评:此题是一个找规律的题目,主要考查了二次根式的性质.观察时,既要注意观察等式的左右两边的联系,还要注意右边必须是一种特殊形式.

练习册系列答案
相关题目