题目内容
19.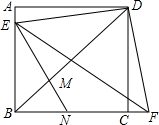 如图,E为正方形ABCD的边AB上一点,F为BC延长线上一点,CF=AE,M为BD上一点,直线EM交BC于N,且DM=DF.
如图,E为正方形ABCD的边AB上一点,F为BC延长线上一点,CF=AE,M为BD上一点,直线EM交BC于N,且DM=DF.(1)求∠DEF的度数;
(2)求证:EN平分∠BEF.
分析 (1)先根据SAS证明△ADE≌△CDF,得出DE=DF,∠ADE=∠CDF,证出∠EDF=∠ADC=90°,得出∠DEF=45°;
(2)先证DE=DM,得出∠DEM=∠DME,再由外角关系证出∠NEF=∠BEM,即可得出结论.
解答 (1)解:∵四边形ABCD是正方形,
∴AD=CD,∠A=∠BCD=∠ADC=90°,
∴∠DCF=90°,
在△ADE和△CDF中,$\left\{\begin{array}{l}{AD=CD}&{\;}\\{∠A=∠DCF=90°}&{\;}\\{AE=CF}&{\;}\end{array}\right.$,
∴△ADE≌△CDF(SAS),
∴DE=DF,∠ADE=∠CDF,
∴∠EDF=∠ADC=90°,
∴∠DEF=45°;
(2)证明:∵DM=DF,由(1)得DE=DF,
∴DE=DM,
∴∠DEM=∠DME,
∵∠DEM=∠DEF+∠NEF=45°+∠NEF,∠DME=∠ABD+∠BEM=45°+∠BEM,
∴∠NEF=∠BEM,
∴EN平分∠BEF.
点评 本题考查了正方形的性质、全等三角形的判定与性质以及等腰三角形的判定与性质;证明三角形全等是解决问题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
8.计算(-3)2n+1+3•(-3)2n的结果是( )
| A. | 34n+2 | B. | 2•32n+1 | C. | -2•32n+1 | D. | 0 |
9.计算:a•$\sqrt{2a}$•5$\sqrt{6ab}$的结果是( )
| A. | 10a2$\sqrt{3b}$ | B. | 60a3b | C. | 5a2$\sqrt{12b}$ | D. | 5a$\sqrt{12b}$ |
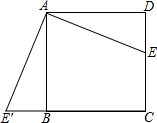 如图,在正方形ABCD中,点E为CD中点,把△ADE绕点A顺时针旋转90°,得到△ABE′,AE′=$\sqrt{5}$,则四边形AECE′的面积为4.
如图,在正方形ABCD中,点E为CD中点,把△ADE绕点A顺时针旋转90°,得到△ABE′,AE′=$\sqrt{5}$,则四边形AECE′的面积为4.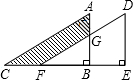 如图,将直角△ABC沿CB方向平移BE的距离得到直角△DEF,已知AG=2,BE=4,DE=6,求图中阴影部分的面积.
如图,将直角△ABC沿CB方向平移BE的距离得到直角△DEF,已知AG=2,BE=4,DE=6,求图中阴影部分的面积. 已知:如图,AB∥CD,∠1=∠2,求证:∠B=∠D.
已知:如图,AB∥CD,∠1=∠2,求证:∠B=∠D.