Question

如图9, 已知抛物线与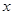轴交于A (－4，0) 和B(1，0)两点，与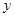轴交于C（0，-2）点．
【小题1】求此抛物线的解析式；
【小题2】设G是线段BC上的动点，作GH//AC交AB于H，连接CF，当△BGH的面积是△CGH面积的3倍时，求H点的坐标;
【小题3】若M为抛物线上A、C两点间的一个动点，过M作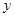轴的平行线，交AC于N，当M点运动到什么位置时，线段MN的值最大，并求此时M点的坐标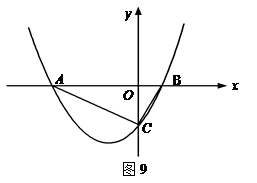

Answer 1

【小题1】设二次函数解析式为y=a(x－x₁)(x－x₂)
∵二次函数与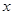轴交于、两点可得：
　　　　　　∴x₁ =－4    x₂=1……………………………………………….1分
∴y=a(x+4)(x－1)
把C（0，-2）代入y=a(x+4)(x－1)得：a=
　　　　　　故所求二次函数的解析式为y= (x+4)(x－1)
=x²+x－2．
【小题2】∵S_△BGH ="2" S_△CGH
……………………………………………4分
∵GH//AC, ,
        ∴△BGH～△BAC,
 ……………6分
故E点的坐标为(，0).    ………………………….7分
【小题3】若设直线的解析式为
∵ A、两点的坐标分别为（－4,0）、（0，－2）．
则有　解得：  
故直线的解析式为．……………………8分       
若设M点的坐标为，又N点是过点M所作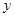轴的平行线与直线的交点，则N点的坐标为（．则有：
　　　　　　　MN=＝
＝……………………………………….9分
即当时，线段MN取大值，此时M点的坐标为（－2，－3）…………10分

解析