题目内容
【题目】已知,如图1在锐角△ABC中,∠ABC=45°,AD⊥BC于点D,BE⊥AC于点E,BE与AD交于点F.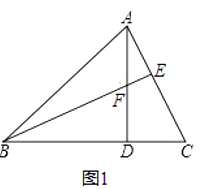
(1)若BF=5,DC=3,求AB的长;
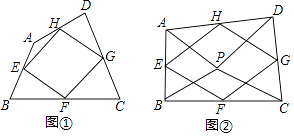
(2)在图1上过点F作BE的垂线,过点A作AB的垂线,链条垂线交于点G,连接BG,得如图2.
①求证:∠BGF=45°;
②求证:AB=AG+ ![]() AF.
AF.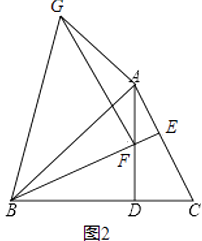
【答案】
(1)解:如图1中,
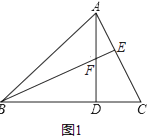
∵∠ABC=45°,AD⊥BC,
∴∠ADB=90°,△ADB是等腰直角三角形,
∴AD=BD,
∵BE⊥AC,
∴∠AEF=∠BDF=90°,
∵∠AFE=∠BFD,
∴∠EAF=∠FBD,∵∠BDF=∠ADC=90°,
∴△BDF≌△ADC,
∴DF=DC=3,
在Rt△BDF中,BD= ![]() =4,
=4,
∴AB= ![]() BD=4
BD=4 ![]()
(2)①证明:如图2中,设AB交GF于O.
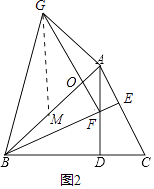
∵∠GAO=∠OFB=90°,∠AOG=∠BOF,
∴△AOG≌△FOB,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,∵∠BOG=∠AOF,
,∵∠BOG=∠AOF,
∴△BOG∽△FOA,
∴∠BGO=∠OAF=45°,
∴∠BGF=45°.
②证明:如图2中,在AB上截取AM=AG,则∠MGA=∠BGF=45°,
∴∠BCM=∠FCA,
∵BC= ![]() FG,GM=
FG,GM= ![]() AC,
AC,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴△BGM∽△FGA,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴BM= ![]() AF,
AF,
∴AB=AM+BM=AG+ ![]() AF.
AF.
【解析】①根据题意得到△ADB是等腰直角三角形,得到AD=BD,得到△BDF≌△ADC,得到DF=DC=3,根据勾股定理求出BD =4,得到AB= ![]() BD=4
BD=4 ![]() ;②在AB上截取AM=AG,则∠MGA=∠BGF=45°,得到∠BCM=∠FCA,得出△BGM∽△FGA,求出BM=
;②在AB上截取AM=AG,则∠MGA=∠BGF=45°,得到∠BCM=∠FCA,得出△BGM∽△FGA,求出BM= ![]() AF,求出AB=AM+BM=AG+
AF,求出AB=AM+BM=AG+ ![]() AF.
AF.
【考点精析】根据题目的已知条件,利用相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

 阅读快车系列答案
阅读快车系列答案