题目内容
 已知反比例函数y=
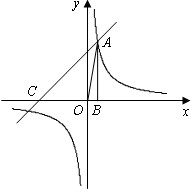
已知反比例函数y= 和一次函数y=2x-1,其中一次函数的图象过(a,b)、(a+1,b+k)两点.如图,已知两个函数图象在第一象限内的交点为A点,在x轴上存在点P,使△AOP为等腰三角形,则P坐标是________.
和一次函数y=2x-1,其中一次函数的图象过(a,b)、(a+1,b+k)两点.如图,已知两个函数图象在第一象限内的交点为A点,在x轴上存在点P,使△AOP为等腰三角形,则P坐标是________.
( ,0),(-
,0),(- ,0),(2,0),(1,0)
,0),(2,0),(1,0)
分析:把过一次函数的两个点代入一次函数,即可求得k,进而求得反比例函数的解析式,因为A点同时在这两个函数解析式上,让这两个函数组成方程组求解即可得到A点坐标,然后求出OA的距离,再根据:OA=OP,OA=AP,OP=AP,分情况讨论解决.
解答: 解:将(a,b)、(a+1,b+k)分别代入一次函数y=2x-1解析式得
解:将(a,b)、(a+1,b+k)分别代入一次函数y=2x-1解析式得
 ,
,
解得k=2,
∴反比例函数解析式为y= ;
;
将y= 和一次函数y=2x-1组成方程组得
和一次函数y=2x-1组成方程组得 ,
,
解得 ,
, ,
,
∵点A在第一象限,
∴点A的坐标为(1,1).
∴OA= =2,OA与x轴所夹锐角为45°,
=2,OA与x轴所夹锐角为45°,
①当OA为腰时,由OA=OP1得P1( ,0),
,0),
由OA=OP2得P2(- ,0);
,0);
由OA=AP3得P3(2,0).
②当OA为底时,OP4=AP4得P4(1,0).
∴符合条件的点有4个,分别是( ,0),(-
,0),(- ,0),(2,0),(1,0).
,0),(2,0),(1,0).
故答案为( ,0),(-
,0),(- ,0),(2,0),(1,0).
,0),(2,0),(1,0).
点评:本题考查了反比例函数的相关问题,在这条直线上的各点的坐标一定适合这条直线的解析式.同时在两个函数解析式上,应是这两个函数解析式的公共解.答案较多时,应有规律的去找不同的解.
 ,0),(-
,0),(- ,0),(2,0),(1,0)
,0),(2,0),(1,0)分析:把过一次函数的两个点代入一次函数,即可求得k,进而求得反比例函数的解析式,因为A点同时在这两个函数解析式上,让这两个函数组成方程组求解即可得到A点坐标,然后求出OA的距离,再根据:OA=OP,OA=AP,OP=AP,分情况讨论解决.
解答:
 解:将(a,b)、(a+1,b+k)分别代入一次函数y=2x-1解析式得
解:将(a,b)、(a+1,b+k)分别代入一次函数y=2x-1解析式得 ,
,解得k=2,
∴反比例函数解析式为y=
 ;
;将y=
 和一次函数y=2x-1组成方程组得
和一次函数y=2x-1组成方程组得 ,
,解得
 ,
, ,
,∵点A在第一象限,
∴点A的坐标为(1,1).
∴OA=
 =2,OA与x轴所夹锐角为45°,
=2,OA与x轴所夹锐角为45°,①当OA为腰时,由OA=OP1得P1(
 ,0),
,0),由OA=OP2得P2(-
 ,0);
,0);由OA=AP3得P3(2,0).
②当OA为底时,OP4=AP4得P4(1,0).
∴符合条件的点有4个,分别是(
 ,0),(-
,0),(- ,0),(2,0),(1,0).
,0),(2,0),(1,0).故答案为(
 ,0),(-
,0),(- ,0),(2,0),(1,0).
,0),(2,0),(1,0).点评:本题考查了反比例函数的相关问题,在这条直线上的各点的坐标一定适合这条直线的解析式.同时在两个函数解析式上,应是这两个函数解析式的公共解.答案较多时,应有规律的去找不同的解.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
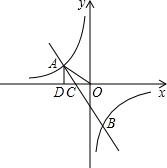 的横坐标为
的横坐标为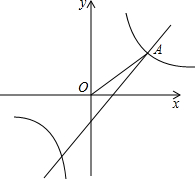 已知反比例函数y=
已知反比例函数y= 和一次函数y2=ax+b的图象相交于第一象限内的点A,且点A的横坐标为1.过点A作AB⊥x轴于点B,△AOB的面积为2.一次函数y2=ax+b的图象与x轴相交于点C,且三角形ABC是等腰直
和一次函数y2=ax+b的图象相交于第一象限内的点A,且点A的横坐标为1.过点A作AB⊥x轴于点B,△AOB的面积为2.一次函数y2=ax+b的图象与x轴相交于点C,且三角形ABC是等腰直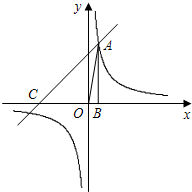 角三角形.
角三角形. ,AD=
,AD= OD,点B
OD,点B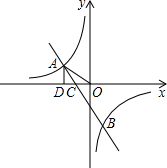 的横坐标为
的横坐标为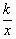 和一次函数y2=ax+b的图象相交于第一象限内的点A,且点A的横坐标为1,过点A作AB⊥x轴于点B,△AOB的面积为2,一次函数y2=ax+b的图象与x轴相交于点C,且三角形ABC是等腰直角三角形。
和一次函数y2=ax+b的图象相交于第一象限内的点A,且点A的横坐标为1,过点A作AB⊥x轴于点B,△AOB的面积为2,一次函数y2=ax+b的图象与x轴相交于点C,且三角形ABC是等腰直角三角形。