题目内容
直线l交反比例函数
的图象于点A，交x轴于点B，点A、B与坐标原点o构成等边三角形，则直线l的函数解析式为 ________或 ________．
y=-
（x+2） y=-（x-2）
分析：首先由题意得到直线与反比例函数y=
的图象相切，则得直线的斜率为-；所以设直线的解析式为：y=-（x+b），与y=组成方程组，根据判别式为0，分析求解即可．
解答：由题意可知直线与反比例函数y=的图象相切，
∴当B点在x轴正方向时，A点在第一象限，当B点在x轴负方向时，A点在第三象限，
∴直线的斜率为-，
设直线的解析式为：y=-（x+b），
代入y=，
得：x2+bx+1=0，
∵只有一个交点，
∴判别式：△=b2-4=0，
∴b=±2，
∴直线的解析式为：y=-（x+2）或y=-（x-2）．
故答案为：y=-（x+2）或y=-（x-2）．
点评：此题考查了一次函数与反比例函数的综合应用．题目难度较大，解题时要注意方程思想、分类讨论与数形结合思想的应用．
（x+2） y=-（x-2）分析：首先由题意得到直线与反比例函数y=
的图象相切，则得直线的斜率为-；所以设直线的解析式为：y=-（x+b），与y=组成方程组，根据判别式为0，分析求解即可．解答：由题意可知直线与反比例函数y=
的图象相切，∴当B点在x轴正方向时，A点在第一象限，当B点在x轴负方向时，A点在第三象限，
∴直线的斜率为-
，设直线的解析式为：y=-
（x+b），代入y=
，得：x2+bx+1=0，
∵只有一个交点，
∴判别式：△=b2-4=0，
∴b=±2，
∴直线的解析式为：y=-
（x+2）或y=-（x-2）．故答案为：y=-
（x+2）或y=-（x-2）．点评：此题考查了一次函数与反比例函数的综合应用．题目难度较大，解题时要注意方程思想、分类讨论与数形结合思想的应用．
练习册系列答案
相关题目
如图，在平面直角坐标系xOy中，等腰直角三角形AOB的直角顶点与原点O重合，点A、B分别在x、y轴上，且AB=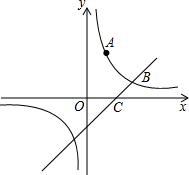
已知：如图反比例函数的图象经过点A、B，点A的坐标为（1，3），点B的纵坐标为1，点C的坐标为（2，0）．直线BC交反比例函数的图象于点D．
已知：如图反比例函数的图象经过点A、B，点A的坐标为（1，3），点B的纵坐标为1，点C的坐标为（2，0）．直线BC交反比例函数的图象于点D．
如图，在平面直角坐标系xOy中，等腰直角三角形AOB的直角顶点与原点O重合，点A、B分别在x、y轴上，且AB=
．直线AB交反比例函数的图象于点C，且AB=2BC．过点C作CD⊥y轴于点D．