题目内容
在半径为13的⊙O中,弦AB∥CD,弦AB和CD的距离为7,若AB=24,则CD的长为
- A.10
- B.4

- C.10或4

- D.10或2

D
分析:根据题意画出图形,由于AB和CD的位置不能确定,故应分AB与CD在圆心O的同侧和AB与CD在圆心O的异侧两种情况进行讨论.
解答: 解:当AB与CD在圆心O的同侧时,如图1所示:
解:当AB与CD在圆心O的同侧时,如图1所示:
过点O作OF⊥CD于点F,交AB于点E,连接OA,OC,
∵AB∥CD,OF⊥CD,
∴OE⊥AB,
∴AE= AB=
AB= ×24=12,
×24=12,
在Rt△AOE中,
OE= =
= =5,
=5,
∴OF=OE+EF=5+7=12,
在Rt△OCF中,CF=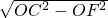 =
= =5,
=5,
∴CD=2CF=2×5=10;
当AB与CD在圆心O的异侧时,如图2所示:
过点O作OF⊥CD于点F,反向延长交AB于点E,连接OA,OC,
∵AB∥CD,OF⊥CD,
∴OE⊥AB,
∴AE= AB=
AB= ×24=12,
×24=12,
在Rt△AOE中,
OE= =
= =5,
=5,
∴OF=EF-OE=7-5=2,
在Rt△OCF中,CF=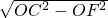 =
= =
= ,
,
∴CD=2CF=2× =2
=2 .
.
故CD的长为10或2 .
.
故选D.
点评:本题考查的是垂径定理,在解答此类题目时要注意进行分类讨论,不要漏解.
分析:根据题意画出图形,由于AB和CD的位置不能确定,故应分AB与CD在圆心O的同侧和AB与CD在圆心O的异侧两种情况进行讨论.
解答:
 解:当AB与CD在圆心O的同侧时,如图1所示:
解:当AB与CD在圆心O的同侧时,如图1所示:过点O作OF⊥CD于点F,交AB于点E,连接OA,OC,
∵AB∥CD,OF⊥CD,
∴OE⊥AB,
∴AE=
 AB=
AB= ×24=12,
×24=12,在Rt△AOE中,
OE=
 =
= =5,
=5,∴OF=OE+EF=5+7=12,
在Rt△OCF中,CF=
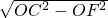 =
= =5,
=5,∴CD=2CF=2×5=10;
当AB与CD在圆心O的异侧时,如图2所示:
过点O作OF⊥CD于点F,反向延长交AB于点E,连接OA,OC,
∵AB∥CD,OF⊥CD,
∴OE⊥AB,
∴AE=
 AB=
AB= ×24=12,
×24=12,在Rt△AOE中,
OE=
 =
= =5,
=5,∴OF=EF-OE=7-5=2,
在Rt△OCF中,CF=
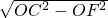 =
= =
= ,
,∴CD=2CF=2×
 =2
=2 .
.故CD的长为10或2
 .
.故选D.
点评:本题考查的是垂径定理,在解答此类题目时要注意进行分类讨论,不要漏解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
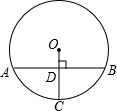 (2012•湛江)如图,在半径为13的⊙O中,OC垂直弦AB于点D,交⊙O于点C,AB=24,则CD的长是
(2012•湛江)如图,在半径为13的⊙O中,OC垂直弦AB于点D,交⊙O于点C,AB=24,则CD的长是