题目内容
我们对多项式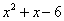 进行因式分解时,可以用待定系数法求解.例如,我们可以先设
进行因式分解时,可以用待定系数法求解.例如,我们可以先设 ,显然这是一个恒等式.根据多项式乘法将等式右边展开有:
,显然这是一个恒等式.根据多项式乘法将等式右边展开有: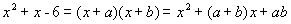
所以,根据等 式两边对应项的系数相等,可得:
式两边对应项的系数相等,可得: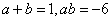 ,解得
,解得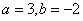 或者
或者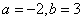 .所以
.所以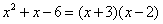 .当然这也说明多项式
.当然这也说明多项式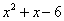 含有因式:
含有因式: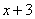 和
和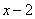 .
.
像上面这种通过利用恒等式的性质来求未知数的方法叫做待定系数法.
利用上述材料及示例解决以下问题.
(1)已知关于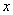 的多项式
的多项式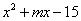 有一个因式为
有一个因式为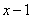 ,求
,求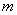 的值;
的值;
(2)已知关于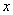 的多项式
的多项式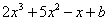 有一个因式为
有一个因式为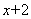 ,求
,求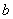 的值.
的值.
|

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
一辆汽车在笔直的公路上行驶,在两次转弯后,前进的方向仍与原来相同,那么这两次
转弯的角度可以是( )
|
| A. | 先右转60°,再左转120° | B. | 先左转120°,再右转120° |
|
| C. | 先左转60°,再左转120° | D. | 先右转60°,再右转60° |
 ,则
,则 ”是假命题的一个反例可以是x = .
”是假命题的一个反例可以是x = . 解: ∵ EF//AD (已知)
解: ∵ EF//AD (已知) =____
=____  年
年 月
月 日在中国上映,获
日在中国上映,获 万人民币票房,请将这个数
万人民币票房,请将这个数 记”为主题的校读书节暨文化艺术节.为了解初中学生更喜欢下列A、B、C、D哪个比赛,从初中学生中随机抽取了部分学生进行调查,每个参与调查的学生只选择最喜欢的一个项目,并将调查结果绘制了两幅不完整的统计图,请回答下列问题:
记”为主题的校读书节暨文化艺术节.为了解初中学生更喜欢下列A、B、C、D哪个比赛,从初中学生中随机抽取了部分学生进行调查,每个参与调查的学生只选择最喜欢的一个项目,并将调查结果绘制了两幅不完整的统计图,请回答下列问题: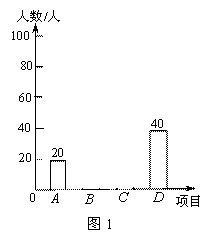


 1、⊙O2的半径O2P2都与x轴垂直,且点P1、P2在反比例函数
1、⊙O2的半径O2P2都与x轴垂直,且点P1、P2在反比例函数 的图像上,则⊿OP1 P2的面积为( )
的图像上,则⊿OP1 P2的面积为( )
 (x>0)的图象上,过点A作AD⊥y轴于点D,延长AD至点C,使AD=DC,过
(x>0)的图象上,过点A作AD⊥y轴于点D,延长AD至点C,使AD=DC,过 点A作AB⊥x轴于点B,连结BC交y轴于点E.若△ABC的面积为4,则k的值为 .
点A作AB⊥x轴于点B,连结BC交y轴于点E.若△ABC的面积为4,则k的值为 .