题目内容
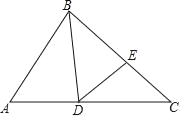
【题目】如图,BD是△ABC的角平分线,点E位于边BC上,已知BD是BA与BE的比例中项.
(1)求证:∠CDE=![]() ∠ABC;
∠ABC;
(2)求证:ADCD=ABCE.
【答案】证明见解析
【解析】试题分析:(1)根据BD是AB与BE的比例中项可得![]() , BD是∠ABC的平分线,则∠ABD=∠DBE,可证△ABD∽△DBE, ∠A=∠BDE. 又因为∠BDC=∠A+∠ABD,
, BD是∠ABC的平分线,则∠ABD=∠DBE,可证△ABD∽△DBE, ∠A=∠BDE. 又因为∠BDC=∠A+∠ABD,
即可证明∠CDE=∠ABD=![]() ∠ABC,(2) 先根据∠CDE=∠CBD,∠C=∠C,可判定
∠ABC,(2) 先根据∠CDE=∠CBD,∠C=∠C,可判定
△CDE∽△CBD,可得![]() .又△ABD∽△DBE,所以
.又△ABD∽△DBE,所以![]() ,
,![]() ,所以
,所以
![]() .
.
试题解析:(1)∵BD是AB与BE的比例中项,
∴![]() ,
,
又BD是∠ABC的平分线,则∠ABD=∠DBE,
∴△ABD∽△DBE,
∴∠A=∠BDE.
又∠BDC=∠A+∠ABD,
∴∠CDE=∠ABD=![]() ∠ABC,即证.
∠ABC,即证.
(2)∵∠CDE=∠CBD,∠C=∠C,
∴△CDE∽△CBD,
∴![]() .
.
又△ABD∽△DBE,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目