题目内容
关于x的函数y=(a-5)x2-4x-1与x轴有交点,则a满足
- A.a≥1
- B.a>1且a≠5
- C.a≥1且a≠5
- D.a≠5
A
分析:因为没有明确函数,所以分二次函数与不是二次函数的情况讨论求解,①是二次函数时,二次函数与x轴有交点,则△≥0,从而可以得出a的取值范围,同时还要考虑二次函数的二次项系数不能为0,②二次项系数等于0,是一次函数时,与x轴是否有交点进行验证,从而得解.
解答:①当a-5≠0,即a≠5,是二次函数时,
∵关于x的函数y=(a-5)x2-4x-1与x轴有交点,
∴b2-4ac=(-4)2-4(a-5)•(-1)=16+4a-20=4a-4≥0,
解得a≥1,
∴a≥1且a≠5,
②当a-5=0,即a=5时,是一次函数y=-4x-1,与x轴有交点(- ,0).
,0).
综上所述,当a≥1时,函数与x轴有交点.
故选A.
点评:此题主要考查了二次函数与坐标轴的交点问题,有一个交点时△=0,有两个交点时△>0,没有交点时△<0,把握住着几个关键,还要考虑二次项系数不能等于0即可,本题没有明确是二次函数,所以a=5时是一次函数也可以,这也是本题容易出错的地方.
分析:因为没有明确函数,所以分二次函数与不是二次函数的情况讨论求解,①是二次函数时,二次函数与x轴有交点,则△≥0,从而可以得出a的取值范围,同时还要考虑二次函数的二次项系数不能为0,②二次项系数等于0,是一次函数时,与x轴是否有交点进行验证,从而得解.
解答:①当a-5≠0,即a≠5,是二次函数时,
∵关于x的函数y=(a-5)x2-4x-1与x轴有交点,
∴b2-4ac=(-4)2-4(a-5)•(-1)=16+4a-20=4a-4≥0,
解得a≥1,
∴a≥1且a≠5,
②当a-5=0,即a=5时,是一次函数y=-4x-1,与x轴有交点(-
 ,0).
,0).综上所述,当a≥1时,函数与x轴有交点.
故选A.
点评:此题主要考查了二次函数与坐标轴的交点问题,有一个交点时△=0,有两个交点时△>0,没有交点时△<0,把握住着几个关键,还要考虑二次项系数不能等于0即可,本题没有明确是二次函数,所以a=5时是一次函数也可以,这也是本题容易出错的地方.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
 (2009•南安市质检)如图,在直角坐标系中,已知点A(0,6),B(8,0).
(2009•南安市质检)如图,在直角坐标系中,已知点A(0,6),B(8,0).
 (2012•朝阳)已知,如图,在平面直角坐标系中,Rt△ABC的斜边BC在x轴上,直角顶点A在y轴的正半轴上,A(0,2),B(-1,0).
(2012•朝阳)已知,如图,在平面直角坐标系中,Rt△ABC的斜边BC在x轴上,直角顶点A在y轴的正半轴上,A(0,2),B(-1,0).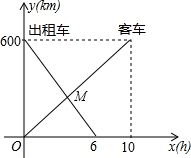 (2013•婺城区一模)一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1(km),出租车离甲地的距离为y2(km),客车行驶时间为x(h),y1,y2与x的函数关系图象如图所示:
(2013•婺城区一模)一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1(km),出租车离甲地的距离为y2(km),客车行驶时间为x(h),y1,y2与x的函数关系图象如图所示: