题目内容
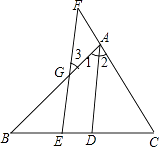
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF. 
(1)求证:AD平分∠BAC;
(2)直接写出AB+AC与AE之间的等量关系.
【答案】
(1)证明:∵DE⊥AB于E,DF⊥AC于F,
∴∠E=∠DFC=90°,
∴△BDE与△CDE均为直角三角形,
∵ ![]()
∴△BDE≌△CDF,
∴DE=DF,即AD平分∠BAC
(2)AB+AC=2AE.
证明:∵BE=CF,AD平分∠BAC,
∴∠EAD=∠CAD,
∵∠E=∠AFD=90°,
∴∠ADE=∠ADF,
在△AED与△AFD中,
∵  ,
,
∴△AED≌△AFD,
∴AE=AF,
∴AB+AC=AE﹣BE+AF+CF=AE+AE=2AE
【解析】(1)根据相“HL”定理得出△BDE≌△CDF,故可得出DE=DF,所以AD平分∠BAC;(2)由(1)中△BDE≌△CDE可知BE=CF,AD平分∠BAC,故可得出△AED≌△AFD,所以AE=AF,故AB+AC=AE﹣BE+AF+CF=AE+AE=2AE.
【考点精析】掌握角平分线的性质定理是解答本题的根本,需要知道定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.

 阅读快车系列答案
阅读快车系列答案【题目】小丽妈妈在网上做淘宝生意,专门销售女式鞋子,一次,小丽发现一个进货单上的一个信息是:A款鞋的进价比B款鞋进价多20元,花500元进A款鞋的数量和花400元进B款鞋的数量相同.
(1)问A、B款鞋的进价分别是多少元?
(2)小丽在销售单上记录了两天的数据如表:
日期 | A款女鞋销量 | B款女鞋销量 | 销售总额 |
6月1日 | 12双 | 8双 | 2240元 |
6月2日 | 8双 | 10双 | 1960元 |
请问两种鞋的销售价分别是多少?
(3)小丽妈妈说:“两款鞋的利润率相同”,请通过计算,结合(1)(2)所给信息,判断小丽妈妈的说法是否正确,如果正确,请说明理由;如果错误,能否只调整其中一款的售价,使得两款鞋的利润率相同?能否同时调整两款的售价,使得两款鞋的利润率相同?请说明理由.