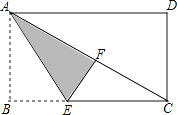
��Ŀ����
����Ŀ����ͼ������AMƽ��������BN����B=90�㣬AB=4��C������BN�ϵ�һ�����㣬����AC����CD��AC����AC=2CD����C��CE��BN��AD�ڵ�E����BC��Ϊa��
��1�����ACD��������ú�a�Ĵ���ʽ��ʾ����
��2�����D������BN�ľ��루�ú���a�Ĵ���ʽ��ʾ����
��3���Ƿ���ڵ�C��ʹ��ACE����AEΪ���ĵ��������Σ������ڣ��������ʱa��ֵ���������ڣ���˵�����ɣ�

���𰸡���1��![]() ����2��
����2��![]() a����3�����ڣ�a��ֵΪ2��4
a����3�����ڣ�a��ֵΪ2��4![]() +8
+8
�������������������1���ȸ��ݹ��ɶ����ó�AC�������ó�CD������������ε������ʽ���ɣ�
��2�����жϳ���FDC=��ACB�������жϳ���DFC�ס�CBA���ó�![]() ���������DF�����ɣ�
���������DF�����ɣ�
��3������������������������ε����ʽ���������⼴�ɵó����ۣ�
�⣺��1����Rt��ABC�У�AB=4��BC=a��
��AC=![]() =
=![]() ��
��
��CD=![]() AC=
AC=![]() ��
��
�ߡ�ACD=90����
��S��ACD=![]() ACCD=
ACCD=![]() .
.
��2����ͼ1������D��DF��BN�ڵ�F��
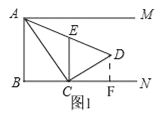
�ߡ�FDC+��FCD=90������FCD+��ACB=180�㩁90��=90����
���FDC=��ACB��
�ߡ�B=��DFC=90����
���FDC=��ACB��
�ߡ�B=��DFC=90����
���DFC�ס�CBA��
��![]() ��
��
��DF=![]() BC=
BC=![]() a��
a��
��D������BN�ľ���Ϊ![]() a��
a��
��3�����ڣ��ٵ�EC=EAʱ��
�ߡ�ACD=90����
��EC=EA=![]() AD��
AD��
��AB��CE��DF��
��BC=FC=a��
�ɣ�2��֪����DFC�ס�CBA��
��![]() ��
��
��FC=![]() AB=2��
AB=2��
��a=2��
�ڵ�AE=ACʱ����ͼ2��AM��CE��
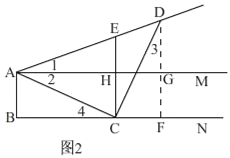
���1=��2��
��AM��BN��
���2=��4��
���1=��4��
�ɣ�2��֪����3=��4��
���1=��3��
�ߡ�AGD=��DFC=90����
���ADG�ס�DCF��
��![]() ��
��
��AD=![]() =
=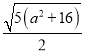 ��AG=a+2��CD=
��AG=a+2��CD=![]() ��
��
��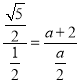 ��
��
��a=4![]() +8��
+8��
��������������a��ֵΪ2��4![]() +8��
+8��