题目内容
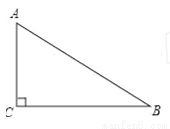
(8分)如图,在Rt△ABC中,∠ACB=90°.
(1)用尺规在边BC上求作一点P,使PA=PB(不写作法,保留作图痕迹);
(2)连结AP,若AC=4,BC=8时,试求点P到AB边的距离.
练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
题目内容
(8分)如图,在Rt△ABC中,∠ACB=90°.
(1)用尺规在边BC上求作一点P,使PA=PB(不写作法,保留作图痕迹);
(2)连结AP,若AC=4,BC=8时,试求点P到AB边的距离.

 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案